BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG TÍCH PHÂN GIẢI QUYẾT BÀI TOÁN THỰC TẾ VỀ TÍNH THỂ TÍCH
- 24/12/2018
- 2,381 lượt xem
Hiện nay các bài toán thực tế đang rất được quan tâm chú trọng thường được đưa vào các kỳ thi và các bài toán thực tế trong đề thi THPT Quốc Gia thường gây khó khăn cho các thí sinh. Trong bài viết lần này, Diễn đàn máy tính cầm tay muốn giới thiệu đến bạn đọc một vài ví dụ cơ bản về ứng dụng tích phân vào tính thể tích trong bài toán thực tế.
Bài toán 1: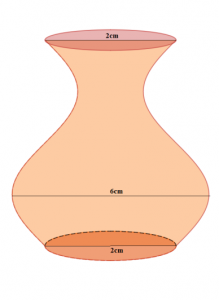
Tính thể tích cái bình hoa với kích thước như hình vẽ biết bình cao $latex 2\pi \left( cm \right)$ và đường sinh của bình khi nằm ngang là đường cong có dạng $latex y=\text{sinx}+2$
Phân tích:
Cái bình có dạng khối tròn xoay với đường sinh hình Parabol là đồ thị của hàm số $latex y=\text{sinx}+2$. Do đó ta có thể áp dụng công thức tích phân để tính thể tích khố tròn xoay trên.
Để việc tính toán trở nên thuận lợi ta nên xây dựng hệ trục tọa độ $latex Oxy$ cho bình nằm ngang và trục $latex Oxy$ chia bình thành hai phần bằng nhau
Hướng dẫn giải
Xây dựng hệ trục tọa độ như hình vẽ: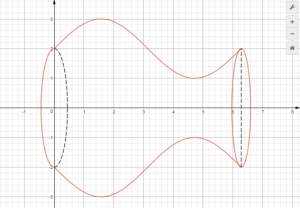
Khi đó thể tích của bình bằng: $latex V=\pi \int\limits_{0}^{2\pi }{{{\left( \operatorname{s}\text{inx}+2 \right)}^{2}}}dx$
Sử dụng máy tính CASIO fx- 580VN X tính tích phân $latex \int\limits_{0}^{2\pi }{{{\left( \operatorname{s}\text{inx}+2 \right)}^{2}}}dx$
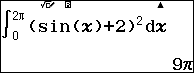
(Trước khi thực hiện phép tính thể tích cần chuyển máy về chế độ Radian )
Vậy thể tích bình hoa $latex V=9{{\pi }^{2}}(c{{m}^{3}})$
Bài toán 2: Một cái lu có bán kính ở 2 đầu là $latex 2\left( dm \right)$và ở giữa là $latex 4\left( dm \right)$, chiều cao của cái lu là $latex 8\left( dm \right)$. Tính lượng nước tối đa mà lu có thể chứa được.
Phân tích: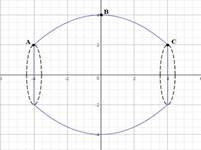
Cái lu có dạng khối tròn xoay với đường sinh hình Parabol là đồ thị của hàm số $latex y=a{{x}^{2}}+bx+c\left( a\ne 0 \right)$. Do đó ta có thể áp dụng công thức tích phân để tính thể tích khối tròn xoay trên.
Dựa vào kích thước của cái lu trên đề bài ta có thể xây dựng hệ trục tọa độ $latex Oxy$ phù hợp và đơn giản như hình vẽ. Khi đó ta có thể sử dụng công thức tích phân để tính thể tích
- Từ chiều cao của cái lu ta tìm được cận của tích phân
- Từ độ dài bán kính 2 đầu và ở giữa ta lấy được 3 điểm $latex A\left( -4;2 \right)$; $latex B\left( 0;4 \right)$; $latex C\left( 4;2 \right)$thuộc đồ thị $latex \left( P \right)$
Hướng dẫn giải:
Tìm phương trình Parabol $latex \left( P \right):y=a{{x}^{2}}+bx+c\left( a\ne 0 \right)$ qua 3 điểm $latex A\left( -4;2 \right)$; $latex B\left( 0;4 \right)$; $latex C\left( 4;2 \right)$
Giải hệ phương trình:
$latex \left\{ \begin{align} & 16a-4b+c=2 \\ & c=4 \\ & 16a+4b+c=2 \\\end{align} \right.$ $latex \Leftrightarrow \left\{ \begin{align} & a=\dfrac{-1}{8} \\& b=0 \\ & c=4 \\\end{align} \right.$ $latex \Rightarrow \left( P \right):y=\dfrac{-1}{8}{{x}^{2}}+4$
Như vậy: $latex V=\pi \int\limits_{-4}^{4}{{{\left( \dfrac{-1}{8}{{x}^{2}}+4 \right)}^{2}}dx}$
Sử dụng máy tính CASIO fx-580VN X tính tích phân trên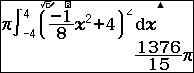
Vậy thể tích cái lu là: $latex V=\dfrac{1376\pi }{15}\approx 288.189\left( d{{m}^{3}} \right)$
Cảm ơn các bạn đã theo dõi bài viết ỨNG DỤNG TÍCH PHÂN GIẢI QUYẾT BÀI TOÁN THỰC TẾ VỀ TÍNH THỂ TÍCH trên. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
