BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG TÍCH PHÂN ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ VỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX
- 25/12/2018
- 963 lượt xem
Hiện nay các bài toán thực tế đang rất được quan tâm chú trọng thường được đưa vào các kỳ thi và các bài toán thực tế trong đề thi THPT Quốc Gia thường gây khó khăn cho các thí sinh. Tiếp nối các bài viết Ứng dụng tích phân vào:Một số bài toán vận tốc; Bài toán thực tế về tính diện tích và Bài toán thực tế về tính thể tích, Diễn đàn máy tính cầm tay muốn giới thiệu thêm đến bạn đọc một số bài toán thực tế có thể giải quyết bằng tích phân
Bài toán thực tế 1: Công ty vừa đưa vào một dây chuyền sản xuất để chế tạo máy tính mới. Sau vài tuần, sản lượng đạt được $latex q\left( t \right)=2000\left[ 1-\dfrac{10}{{{\left( 10-t \right)}^{2}}} \right]$ máy/tuần. Tìm số máy sản xuất được từ đầu tuần thứ ba đến hết tuần thứ tư
A. $latex 147$ máy B. $latex 1523$ máy C. $latex 1470$ máy D. $latex 3166$ máy
Hướng dẫn giải:
Số máy sản xuất được từ đầu tuần thứ ba đến hết tuần thứ tư là: $latex \int\limits_{2}^{4}{2000\left[ 1-\dfrac{10}{{{\left( 10-t \right)}^{2}}} \right]dt}$
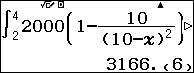
Đáp án D
Bài toán thực tế 2: Người ta thay nước mới cho 1 bể bơi có dạng hình hộp chữ nhật có độ sâu là $latex {{h}_{1}}=300cm$. Giả sử $latex h\left( t \right)$ là chiều cao (tính bằng cm) của mực nước bơm được tại thời điểm $latex t$ giây, biết rằng tốc độ tăng chiều cao mực nước tại giây thứ $latex t$ là $latex {h}’\left( t \right)=\dfrac{1}{500}\sqrt[3]{t+3}$ và lúc đầu hồ bơi không có nước. Hỏi sau bao lâu thì nước bơm được $latex \dfrac{3}{4}$ độ sâu của hồ bơi
A. 2 giờ 7 phút B. 1 giờ 7 phút C. 4 giờ 7 phút D. 3 giờ 7 phút
Hướng dẫn giải:
Mực nước của hồ bơi tại thời gian $latex t$ giây là: $latex h\left( t \right)=h\left( 0 \right)+\int\limits_{0}^{t}{\left( \dfrac{1}{500}\sqrt[3]{x+3} \right)dx}=\int\limits_{0}^{t}{\left( \dfrac{1}{500}\sqrt[3]{x+3} \right)dx}$
Theo đề bài, lượng nước bơm được bằng $latex \dfrac{3}{4}$ độ sâu của hồ bơi nên ta có:
$latex h\left( t \right)=\dfrac{3}{4}{{h}_{1}}\Leftrightarrow \int\limits_{0}^{t}{\left( \dfrac{1}{500}\sqrt[3]{x+3} \right)dx}=\dfrac{3}{4}300=225$
Dùng chức năng SOLVE của Casio fx 580vnx để tìm nghiệm cho phương trình trên:
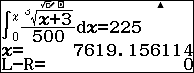
Vậy $latex t\approx 7619\approx $2 giờ 7 phút
Đáp án A
Bài toán thực tế 3: Một công ty dự định đầu tư một khu nhà máy sản xuất. Giả sử sau $latex t$ năm, dự án lần 1 có tốc độ phát sinh lợi nhuận là $latex {{P}_{1}}\left( t \right)=100+{{t}^{2}}$trăm đôla/năm, tiếp sau đó dự án lần 2 có tốc độ phát sinh lợi nhuận là $latex {{P}_{2}}\left( t \right)=150+5t$ trăm đôla/năm. Biết rằng sau thời gian $latex t$ thì tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2. Tính lợi nhuận chênh lệch thực tế cho khoảng thời gian trên
A. $latex 676.66$ trăm đô B. $latex 755$ trăm đô C. $latex 750$ trăm đô D. $latex 666.67$ trăm đô
Hướng dẫn giải
Khoảng thời gian $latex t\left( t>0 \right)$ để tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2 là nghiệm dương của phương trình:
$latex {{P}_{1}}\left( t \right)=2{{P}_{2}}\left( t \right)\Leftrightarrow 100+{{t}^{2}}=300+10t\Leftrightarrow \left[ \begin{align} & t=20 \\ & t=-10 \\\end{align} \right.$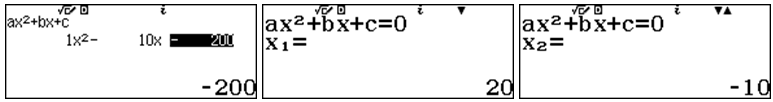
Vậy lợi nhuận chênh lệch thực tế cho khoảng thời gian $latex 0\le t\le 20$ là
$latex \int\limits_{0}^{20}{\left[ {{P}_{1}}\left( t \right)-{{P}_{2}}\left( t \right) \right]}dt=\int\limits_{0}^{20}{\left[ \left( 100+{{t}^{2}} \right)-\left( 150+5t \right) \right]dt=\int\limits_{0}^{20}{\left( {{t}^{2}}-5t-50 \right)dt}}$
Đáp án D
Bài toán thực tế 4: Ban đầu trong một mẫu nước có khoảng $latex 600$con vi khuẩn, trong 1 giờ số lượng này tăng lên với tốc độ $latex v\left( t \right)=400{{e}^{1.25t}}$. Hỏi sau 3 giờ, 5giờ và 7 giờ số lượng vi khuẩn trong mẫu lần lượt là bao nhiêu ?
A. $latex 13886-166044-2019700$ B. $latex 17608-207805-2524875$
C. $latex 18808-210205-2528475$ D. $latex 18702-220350-2516969$
Hướng dẫn giải:
Cách 1
Đặt $latex S\left( t \right)$ là số vi khuẩn trong mẫu sau $latex t$ giờ
Khi đó ta có:
$latex S\left( t \right)=\int{v\left( t \right)dt=\int{400{{e}^{1.25t}}dt=320{{e}^{1.25t}}+C}}$
Theo đề bài ta có:
$latex S\left( 0 \right)=600\Leftrightarrow 320+C=600\Leftrightarrow C=280$
Suy ra: $latex S\left( t \right)=320{{e}^{1.25t}}+280$
Sử dụng Casio fx 580vnx tìm số lượng vi khuẩn sau 3 giờ, 5giờ và 7 giờ
Nhập biểu thức vào máy:
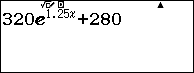
Sử dụng lệnh r lần lượt tại các giá trị $latex x=3$; $latex x=5$ và $latex x=7$
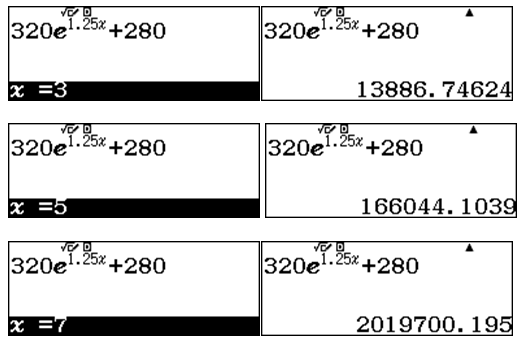
Đáp án A
Cách 2:
Đặt $latex S\left( t \right)$ là số vi khuẩn trong mẫu sau $latex t$ giờ
Ta có $latex S\left( t \right)=S\left( 0 \right)+\int\limits_{0}^{t}{400{{e}^{1.25x}}dx=600+}\int\limits_{0}^{t}{400{{e}^{1.25x}}dx}$
Nhập biểu thức vào máy: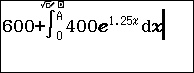
Sử dụng lệnh r lần lượt tại các giá trị $latex A=3$; $latex A=5$ và $latex A=7$
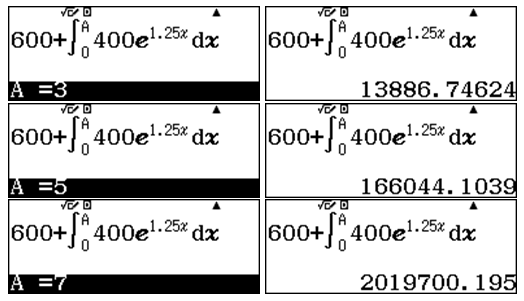
Đáp án A
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG TÍCH PHÂN ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ VỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
