Vấn đề tìm diện tích tam giác và tính bán kính đường tròn nội tiếp tam giác
- 21/10/2021
- 145 lượt xem
Bài 10B. Cho tam giác $ABC$ có $AB = 4,7$, trung tuyến $AM = 5,4$ và đường cao $BH = 3,7$. Gọi $O$ là giao điểm của $AM$ và $BH$. Tính gần đúng (chính xác đến 2 chữ số thập phân):
|
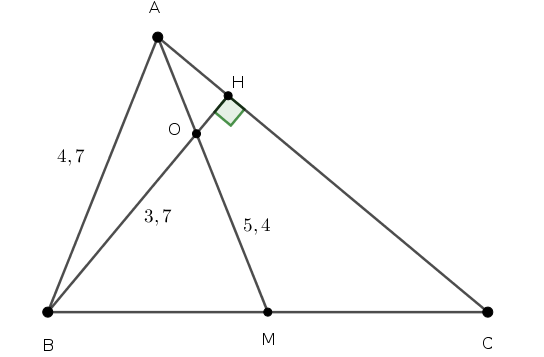
| $$AC=7,25 ; BC=5,71 ; AO=3,08$$ |
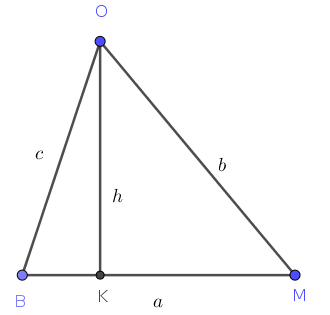
Đặt
$c=OB=$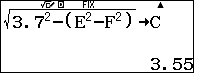
$b=OM=$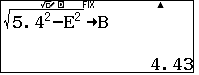
$a=BM=$ $
$
Vì góc $O$ của tam giác $OBM$ nhọn nên chân đường cao từ $O$ nằm trên đoạn $BM$ do đó chiều cao $h$ kẻ từ $O$ của tam giác $OBM$ là nghiệm của phương trình:

Vậy diện tích tam giác $OBM$ là
$$S=\dfrac{1}{2}ah$$

Bán kính đường tròn nội tiếp tam giác $OBM$ xác định bởi công thức $$r=\dfrac{S}{p}=\dfrac{2S}{a+b+c}$$

Chia sẻ
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay