BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm dư của phép chia mà số bị chia là một số cực lớn.
- 22/10/2021
- 574 lượt xem
Thông thường số bị chia có dạng $x=a^{2000+n}$ với $n$ là một số tự nhiên trong khoảng $(0;30)$ để tương ứng với năm diễn ra kỳ thi, ví dụ năm nay $2000+21$.
Ví dụ sau đây trích từ bài thi HSG MTCT THCS TP HCM năm 2021.
| Tìm dư trong phép chia $7^{2020}$ : 2021 |
Cách giải các bài toán thuộc loại này như sau:
-
- 1. Nhận xét:
Do đó $7^{2000}=7^{2^5}.7^{2^6}.7^{2^7}.7^{2^8}.7^{2^9}.7^{2^{10}}.7^{2^2}$
- 2. Ta tìm dư của phép chia $7^{2^2}$ cho $2021$
- 3. Để tìm dư của phép chia $7^{2^5}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$ (3 lần), lưu kết quả vào B.
- 1. Nhận xét:
| Sau đây ta bấm = liên tục để tìm dư, có thể không cần lưu chỉ cần ghi ra giấy cho nhanh. |
- 4. Để tìm dư của phép chia $7^{2^6}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$, lưu kết quả vào C.
- 5. Để tìm dư của phép chia $7^{2^7}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$, lưu kết quả vào D.
- 6. Để tìm dư của phép chia $7^{2^8}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$, lưu kết quả vào E.
- 7. Để tìm dư của phép chia $7^{2^9}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$, lưu kết quả vào x. (tránh biến nhớ F luôn luôn là dư của các phép chia)
- 8. Để tìm dư của phép chia $7^{2^{10}}$ cho $2021$ ta tìm dư của phép chia $F$ cho $2021$, lưu kết quả vào y.
Vậy
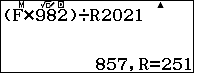
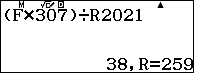
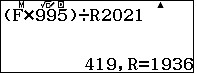
Nghĩa là dư của phép chia $7^{2020}$ cho $2021$ là 294.
Chia sẻ
About TS. Nguyễn Thái Sơn
