Dư của phép chia đa thức $ax^3+bx^2+cx+d$ cho tam thức $x^2+\alpha x+\beta$

Thực hiện phép chia đa thức $\dfrac{ax^3+bx^2+cx+d}{x^2+\alpha x+\beta}$ ta có thương và dư như sau:
$$\dfrac{ax^3+bx^2+cx+d}{x^2+\alpha x+\beta}=ax+b-a\alpha+\dfrac{[c-a\beta -\alpha(b-a\alpha)]x+d-\beta(b-a\alpha))}{x^2+\alpha x+\beta}$$

Vậy dư của phép chia đa thức nói trên là:

Áp dụng: Tìm đa thức bậc ba $f (x )$ sao cho $f (x )$ chia cho $x^2-x+2$ dư $2x-1$, chia cho $x^2+x$ dư $16x-3$. Tính $f(2021)$.
Giải:

1. 1. Với $\alpha=-1, \beta=2$ theo đề bài ta có:
   $$2x-1\equiv [c-a\beta -\alpha(b-a\alpha)]x+d-\beta(b-a\alpha) \Leftrightarrow \left\{\begin{array}{l}(\alpha^2-\beta)a-\alpha b+c=2\\
   \alpha\beta a-\beta b+d=-1\end{array}\right.$$
2. 2. Với $\alpha=1, \beta=0$ theo đề bài ta có:
   $$16x-3\equiv [c-a\beta -\alpha(b-a\alpha)]x+d-\beta(b-a\alpha) \Leftrightarrow \left\{\begin{array}{l}(\alpha^2-\beta)a-\alpha b+c=16\\
   \alpha\beta a-\beta b+d=-3\end{array}\right.$$

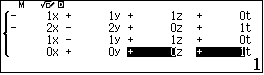
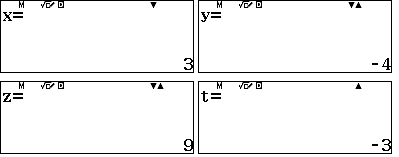
Vậy đa thức bậc ba cần tìm là:

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.