Tìm GTLN và GTNN của A=\sqrt{6-x}+\sqrt{x-3}

08/11/2017
6,528 lượt xem
casiobitex

Đề bài: Tìm GTLN, GTNN của $A=\sqrt{6-x}+\sqrt{x-3}$

Câu hỏi của thành viên trên diễn đàn Toán CASIO

Tìm GTLN và GTNN của $A=\sqrt{6-x}+\sqrt{x-3}$

Bài giải:

Điều kiện: $3\leqslant x\leq 6$ .

Với điều kiện trên thì: $A^{2}=3+2\sqrt{\left ( 6-x \right )\left ( x-3 \right )}=3+\sqrt{-x^{2}+9x-18}$

8 14

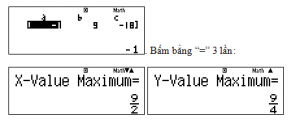
Ta được: $A^{2}=3+2\sqrt{-\left ( x- \frac{9}{2}\right )^{2}+\frac{9}{4}}$

Nhận xét 1: đ $A^{2}$ ạt GTLN khi $\sqrt{-\left ( x- \frac{9}{2}\right )^{2}+\frac{9}{4}}$ đạt GTLN.

Ta có $-\left ( x- \frac{9}{2}\right )^{2}+\frac{9}{4}\leqslant \frac{9}{4}$ . Vậy GTLN của $A^{2}$ là $3+2\sqrt{\frac{9}{4}}=6$ nên GTLN của A là $\sqrt{6}$ và đạt được khi $x=\frac{9}{2}$

Nhận xét 2: : $A^{2}$ ạt GTNN khi $\sqrt{-\left ( x- \frac{9}{2}\right )^{2}+\frac{9}{4}}$ đạt GTNN

GTNN của $\sqrt{-\left ( x- \frac{9}{2}\right )^{2}+\frac{9}{4}}$ là 0 (Vì căn thức luôn không âm)

Do đó, GTNN của A là $\sqrt{3}$ và đạt được khi $x=3$ hoặc $x=6$ .

Chia sẻ

H	B	T	N	S	B	C
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay

Tìm GTLN và GTNN của A=\sqrt{6-x}+\sqrt{x-3}

About casiobitex

Bài viết liên quan

Bài Viết Tương Tự

BỘ ĐỀ ÔN THI CUỐI HỌC KỲ I LỚP 9

BẢN TIN

ĐĂNG KÝ NHẬN BẢN TIN