ỨNG DỤNG PHƯƠNG THỨC VECTOR TRONG CASIO FX580 VNX(V)
- 17/12/2018
- 467 lượt xem
Ở loạt bài viết này chúng tôi đưa ra những hướng dẫn cụ thể từ dễ tới khó về phương thức vector trong máy tính Casio fx580VNX. Từ đó giúp các học sinh giải quyết những bài toán về hình học Oxyz và những bài toán về phương pháp tọa độ trong không gian một cách dễ dàng và nhanh chóng hơn. Ở phần 4 chúng tôi đã đưa ra những tính năng tính toán tổng hợp với phương thức vector. Phần 5 này chúng tôi sẽ ứng dụng phương thức vector để giải một số bài toán trong đề thi thpt quốc gia.
Phần 5: Ứng dụng phương thức vector để giải một số bài toán trong đề thi thpt.
Tóm tắt: Ở loạt bài viết này chúng tôi đưa ra những hướng dẫn cụ thể từ dễ tới khó về phương thức vector trong máy tính Casio fx580VNX. Từ đó giúp các học sinh giải quyết những bài toán về hình học Oxyz và những bài toán về phương pháp tọa độ trong không gian một cách dễ dàng và nhanh chóng hơn. Ở phần 4 chúng tôi đã đưa ra những tính năng tính toán tổng hợp với phương thức vector. Phần 5 này chúng tôi sẽ ứng dụng phương thức vector để giải một số bài toán trong đề thi thpt quốc gia.
Xem lại: PHẦN 4: ỨNG DỤNG PHƯƠNG THỨC VECTOR GIẢI BÀI TOÁN TRONG ĐỀ THI MINH HỌA 2019
8. Giải quyết một số bài toán trong đề thi thpt quốc gia bằng phương thức vector
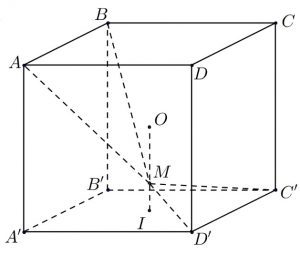 Câu 15(TS-2018). Cho hình lập phương $latex ABCD.A’B’C’D’$ có tâm $latex O$. Gọi $latex I$ là tâm của hình vuông $latex A’B’C’D’$ và $latex M$ là điểm thuộc đường thẳng $latex OI$ sao cho $latex MO=2MI$ (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng $latex \left( MC’D’ \right)$ và $latex \left( MAD \right)$ bằng
Câu 15(TS-2018). Cho hình lập phương $latex ABCD.A’B’C’D’$ có tâm $latex O$. Gọi $latex I$ là tâm của hình vuông $latex A’B’C’D’$ và $latex M$ là điểm thuộc đường thẳng $latex OI$ sao cho $latex MO=2MI$ (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng $latex \left( MC’D’ \right)$ và $latex \left( MAD \right)$ bằng
A. $latex \dfrac{6\sqrt{85}}{85}$. B. $latex \dfrac{7\sqrt{85}}{85}$.
C. $latex \dfrac{17\sqrt{13}}{65}$. D. $latex \dfrac{6\sqrt{13}}{65}$.
Giải
Chọn hệ trục tọa độ $latex Oxyz$ sao cho $latex O\equiv O$, tia $latex Ox//DB;Oy//CA;Oz\equiv IO$.
Khi đó $latex B\left( \dfrac{\sqrt{2}}{2};0;\dfrac{1}{2} \right),A\left( 0;\dfrac{\sqrt{2}}{2};\dfrac{1}{2} \right),M\left( 0;0;-\dfrac{1}{3} \right),C’\left( 0;-\dfrac{\sqrt{2}}{2};-\dfrac{1}{2} \right),D’\left( -\dfrac{\sqrt{2}}{2};0;-\dfrac{1}{2} \right)$
Ta có: $latex \overrightarrow{MA}=\left( 0;\dfrac{\sqrt{2}}{2};\dfrac{5}{6} \right),\overrightarrow{MB}=\left( \dfrac{\sqrt{2}}{2};0;\dfrac{5}{6} \right),\overrightarrow{MC’}=\left( 0;-\dfrac{\sqrt{2}}{2};-\dfrac{1}{6} \right),\overrightarrow{MD’}=\left( -\dfrac{\sqrt{2}}{2};0;-\dfrac{1}{6} \right)$
Nhập 4 vector vào máy tính


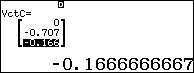
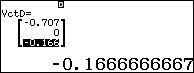
Tính cos của góc tạo bởi hai mặt phẳng

Vì 2 phương án A và B là bội của $latex \dfrac{\sqrt{85}}{85}$ nên ta chia M cho $latex \dfrac{\sqrt{85}}{85}$ (nhân M cho $latex \sqrt{85}$)
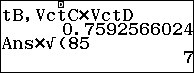
Vậy chọn đáp án B.
Lưu ý: nếu nhân M cho $latex \sqrt{85}$ không ra được số nguyên thì ta chia kết quả cho $latex \dfrac{\sqrt{13}}{65}$ (bội của đáp án C và D).
Câu 16(TS-2018). Trong không gian cho đường thẳng $latex d:\left\{ \begin{align}& x=1+3t \\ & y=1+4t \\ & z=1 \\ \end{align} \right.$. Gọi $latex \Delta $ là đường thẳng đi qua điểm $latex A\left( 1;1;1 \right)$ và có vectơ chỉ phương $latex \overrightarrow{u}=\left( 1;-2;2 \right)$. Đường phân giác của góc nhọn tạo bởi $latex d$ và $latex \Delta $ có phương trình là
A. $latex \left\{ \begin{align}& x=1+7t \\& y=1+t \\ & z=1+5t \\ \end{align} \right.$ B. $latex \left\{ \begin{align} & x=-1+2t \\ & y=-10+11t \\ & z=-6-5t \\ \end{align} \right.$ C. $latex \left\{ \begin{align} & x=-1+2t \\ & y=-10+11t \\ & z=6-5t \\ \end{align} \right.$ D. $latex \left\{ \begin{align} & x=1+3t \\ & y=1+4t \\ & z=1-5t \\ \end{align} \right.$
Giải
Gọi $latex \overrightarrow{v}=\left( 3;4;0 \right)$ là vector chỉ phương của $latex d$
Nhập 2 vector vào máy


Ta có: $latex \overrightarrow{u}.\overrightarrow{v}=-5$

Do đó $latex \overrightarrow{u}$ và $latex \overrightarrow{v}$ hợp với nhau góc tù, vậy $latex \overrightarrow{u}$ và $latex \overrightarrow{v}$ hợp với nhau góc nhọn. Ta sử dụng vector đơn vị

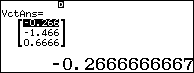
Nhân vector cho 15 ta được


Vậy vector chỉ phương của đường phân giác là $latex \overrightarrow{w}=\left( -4;-22;10 \right)$, ta loại đi đáp án A và D. Chọn $latex t=1$ thì phương án C biểu diễn đường thẳng đi qua điểm $latex A\left( 1;1;1 \right)$. Vậy ta chọn C.
—————————————————-
Bài viết khó tránh khỏi thiếu sót, các bạn có thắc mắc hay bình luận hoặc góp ý thì đừng ngại gửi tin nhắn cho ad trên Fanpage: Diễn Đàn Toán Casio nhá.
Xem tiếp: PHẦN 6: ỨNG DỤNG PHƯƠNG THỨC VECTOR ĐỂ TÍNH CÁC BÀI TOÁN TỔNG HỢP TRÊN CASIO FX580 VNX (VI)
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay