CHINH PHỤC CÁC BÀI TOÁN TỔ HỢP XÁC SUẤT BẰNG MÁY TÍNH CASIO FX-580VNX

03/05/2021
28,538 lượt xem
Toanbitexdtgd1

Bài 1: Có bao nhiêu cách xếp hạng nhất, nhì, ba cho 8 vận động viên thể thao trong một cuộc thi. Biết thành tích 8 vận động viên khác nhau.

Hướng dẫn:

Để xếp vào các vị trí nhất nhì ba ta chọn 3 vận động viên trong 8 vận động viên (có thứ tự). => đây là chỉnh hợp chập 3 của 8.

Vậy $A_{8}^{3}=\frac{8!}{(8-3)!}$ = 336 cách.

Bài 2: Để khuyến khích cho các em học sinh giỏi. Nhà trường thưởng mỗi em 3 dụng cụ học tập được chọn từ: thước, viết, tập, bút chì, sách. Hỏi có bao nhiêu cách trao thưởng như thế.

Hướng dẫn:

Mỗi học sinh được chọn 3 dụng cụ từ 5 dụng cụ ( không cần thứ tự và có thể các dụng cụ giống nhau như: chọn 2 viết và 1 tập). nên đây là tổ hợp có lặp chập 3 của 5.

Vậy $C_{5}^{'3}=C_{7}^{3}$ = 35 cách.

Bài 3: Một lớp có 40 học sinh, trong đó 25 nam và 15 nữ. Chọn ngẫu nhiên 4 học sinh. Hỏi có bao nhiêu cách chọn 4 học sinh đó dự đại hội thể thao trong đó có ít nhất một nam.

Hướng dẫn:

chọn 4 học sinh tùy ý ( nghĩa là có thể 4 học sinh toàn nam, hoặc toàn nữ, hoặc cả hai): $C_{40}^{4}$
chọn 4 học sinh toàn là nữ: $C_{15}^{4}$
vậy : số cách chọn 4 học sinh trong đó có ít nhất một nam là: $S=C_{40}^{4}-C_{15}^{4}=90025$

Bài 4: Đội thanh niên tình nguyện của một trường THPT gồm 15 HS, trong đó có 4 HS khối 12, 5 HS khối 11 và 6 HS khối 10. Chọn ngẫu nhiên 6 HS đi thực hiện nhiệm vụ. Tính xác suất để 6 HS được chọn có đủ 3 khối.

Hướng dẫn:

Số phần tử của không gian mẫu $n\left( \Omega \right)=C_{15}^{6}=5005$ .

Gọi A là biến cố: “6 HS được chọn có đủ 3 khối”.

Xét các trường hợp của biến cố $\overline{A}$

+ Số cách chọn được 6 HS bao gồm cả khối 10 và 11: $C_{11}^{6}-C_{6}^{6}$

+ Số cách chọn được 6 HS bao gồm cả khối 10 và 12: $C_{10}^{6}-C_{6}^{6}$

+ Số cách chọn được 6 HS bao gồm cả khối 11 và 12: $C_{9}^{6}$

+ Số cách chọn được 6 HS khối 10: $C_{6}^{6}$

Vậy $n\left( \overline{A} \right)=C_{11}^{6}+C_{10}^{6}+C_{9}^{6}-C_{6}^{6}=755\Rightarrow n\left( A \right)=5005-755=4250$

Vậy xác suất cần tìm là: $P\left( A \right)=\frac{4250}{5005}=\frac{850}{1001}.$

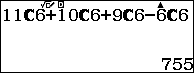
Bài 5: Cho tập $A=\left\{ 1;2;3;4;5;6 \right\}$ . Tính xác suất biến cố chọn được số tự nhiên có 3 chữ số khác nhau lập từ tập A, sao cho tổng 3 chữ số bằng 9.