BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Thắc mắc hỏi Thầy Sơn
- 04/05/2021
- 254 lượt xem
Thắc mắc của Thầy Hiền thú vị nhưng không phải lạ vì cách đây nhiều năm nhiều người đã hỏi và Thầy đã trả lời. Hôm nay Thầy Sơn sẽ trả lời lại và qua đó lưu ý các bạn một số vấn đề về số cực lớn trên máy tính Casio FX580 VNX.
Về phương diện thuật toán, để tính giá trị của một biểu thức chứa biến $x$ lập trình viên sẽ code để máy tính sẽ tính toán tuần tự các phép toán. Ở đây $f(x)=x^5-2019x^4+2019x^3-2019x^2+2019x-1000$ với $x=1008$, trước hết máy tính sẽ tính $x^5=2018^5=$ 
, số này có 17 chữ số nên tràn bộ nhớ (máy tính Casio (mọi phiên bản) đều chỉ nhớ đến 15 chữ số), máy tính cá nhân (PC) nhớ đến 16 chữ số. Vì vậy nó sẽ làm tròn kết quả này đến chữ số thứ 15.
Sau đó máy tính sẽ tiếp tục quá trình trên cho đến hết.
Vì làm tròn nhiều lần nên kết quả sẽ được khuyến cáo là không đúng với giá trị thật của nó.
Khi dạy cho học sinh sử dụng máy tính cầm tay, các giáo viên phải nói rõ điều này cho học sinh. Riêng người ra đề thi HSG MTCT sẽ không nên ra những bài toán như vậy vì sẽ bị xem là đánh lừa thí sinh vốn không hiểu sự kiện nói trên.
Vậy bài toán trên thực hiên trên máy tính Casio FX580VNX như thế nào? Đơn giản nhất là không tính $x^5$. Hãy đặt thừa số chung để lộ diện tối đa $x^4$. Vì $x^4$ sẽ không tràn bộ nhớ nếu $x$ tối đa vào khoảng $4000$. Do đó một đa thức bậc 4 theo biến $x$ với $x=2018$ chẳng hạn, kết qủa tính toán sẽ chính xác.
Lời giải:
$f(x)=x(x^4-2019x^3+2019x^2-2019x+2019)-1000$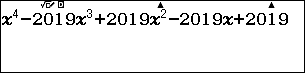 
khi thay $x=2018$ vào đa thức bậc 4, kết quả là
Vậy $f(2018)=2018-1000=1018$.
Vấn đề tương tự: Tính $123456789^2$
Thao tác trên máy tính Casio FX580VNX
nghĩa là $123456789^2=15241578750190500$ (sai) và các bạn thấy máy tính nó làm tròn kết qủa đến chữ số thứ 15.
Lời giải đúng trên máy tính Casio
$123456789^2=(123456780+9)^2=15241576527968400+81+18\times 123456780=$
Tóm lại: $123456789^2=152415768750190521$
About TS. Nguyễn Thái Sơn
