BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BÀI TOÁN TÍCH PHÂN THƯỜNG GẶP TRONG ĐỀ THI TOÁN THPT QUỐC GIA
- 12/06/2019
- 775 lượt xem
Tích phân là một chuyên đề luôn xuất hiện trong các đề thi THPT Quốc Gia với nhiều câu hỏi từ mức độ nhận biết đến vận dụng cao. Trong bài viết này, Diễn đàn sẽ chia sẻ đến bạn đọc 1 bài toán tích phân thường xuất hiện trong đề thi THPT Quốc Gia
Tích phân là một chuyên đề luôn xuất hiện trong các đề thi THPT Quốc Gia với nhiều câu hỏi từ mức độ nhận biết đến vận dụng cao. Trong bài viết này, Diễn đàn sẽ chia sẻ đến bạn đọc 1 bài toán tích phân thường xuất hiện trong đề thi THPT Quốc Gia
Bài toán ( trích từ đề thi thử chuyên Vinh)
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ thỏa mãn $f(0)=3$ và $f(x)+f(2-x)=x^{2}-2 x+2, \forall x \in \mathbb{R}$. Tích phân $\int\limits_{0}^{2}xf^{\prime}(x)dx$ bằng
A. $\dfrac{5}{3}$. B. $-\dfrac{4}{3}$ C. $-\dfrac{10}{3}$. D. $\dfrac{2}{3}$.
[/dropshadowbox]Hướng dẫn giải
Theo đề bài ta có $f(0)+f(2)=2 \Rightarrow f(2)=2-f(0)=2-3=-1$
Ta có $\int\limits_{0}^{2} f(x) \mathrm{d} x=\int\limits_{0}^{2} f(2-x) \mathrm{d} x$
và $\int\limits_{0}^{2}(f(x)+f(2-x)) \mathrm{d} x=\int\limits_{0}^{2}\left(x^{2}-2 x+2\right) \mathrm{d} x=\dfrac{8}{3} $
Suy ra $ \int\limits_{0}^{2} f(x) \mathrm{d} x=\dfrac{4}{3}$
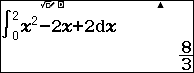
Theo công thức tích phân từng phần ta có:
$$\int\limits_{0}^{2} x f^{\prime}(x) \mathrm{d} x=x f\left.(x)\right|_{0} ^{2}-\int\limits_{0}^{2} f(x) \mathrm{d} x=2 .(-1)-\dfrac{4}{3}=-\dfrac{10}{3}$$
Đáp án C
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
