THỰC HÀNH GIẢI QUYẾT BÀI TOÁN TÀI CHÍNH: NIÊN KIM (DÀNH CHO HS GIỎI) - P1
- 04/07/2019
- 422 lượt xem
Bài toán 1:
Anh A muốn mua căn nhà có giá trị 600.000.000 VNĐ và anh ta cần trả trước 100.000.000 VNĐ, còn lại 500.000.000 VNĐ anh vay ngân hàng và sẽ trả trong vòng 10 năm với lãi kép 7.2% hàng tháng.
|
Giải
1) 
Lãi kép 7.2% hàng tháng, nghĩa là lãi kép 7.2% một năm, kỳ hạn một tháng.
$n=10\times 12=120, i=7.2, PV=500000000$ ($PV>0$ là khoản vay, $PV<0$ là số tiền nộp vào). Kỳ hạn một tháng nên $P/Y=12$. Ngoài ra $C/Y=P/Y$.
Bấm F4  $\approx 5.857.094$VNĐ
$\approx 5.857.094$VNĐ
2) Ta có $R=P\times \dfrac{i}{1-(1+i)^{-n}} \quad (1)$
Số dư nợ theo kỳ hạn thứ $p$ của khoản vay cho bởi công thức:
$$D= P(1+i)^p-\dfrac{R}{i}\left[(1+i)^p-1\right] \quad (2)$$
trong đó $p$ là số thứ tự của kỳ hạn thanh toán, $1\leqslant p\leqslant n$.
Thay (1) vào (2)
$$D=P(1+i)^p-\dfrac{P}{1-(1+i)^{-n}}\left[(1+i)^p-1\right]$$
$$\Leftrightarrow D=\dfrac{P}{1-(1+i)^{-n}}\left[(1+i)^p-(1+i)^{p-n}-(1+i)^p+1\right] $$
Vậy: $$D=P\times \dfrac{1-(1+i)^{p-n}}{1-(1+i)^{-n}}$$
3) Thao tác trên máy tính Casio fx-9860 GII SD, bảng với 120 dòng
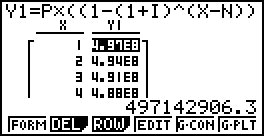
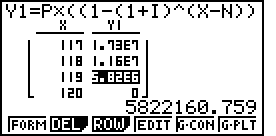
Trên MS Excel hoặc LibreOffice Calc
 Loading...
Loading...
Bài toán 2:
| Giả sử một người muốn lập một quỹ hưu (một tài khoản trong ngân hàng dành riêng cho việc trả lương hưu về sau). Người này sẽ làm việc 30 năm nữa, và mỗi tháng sẽ rót vào quỹ hưu một khoản tiền đều đặn trong vòng 30 năm làm việc. Khi về hưu (30 năm sau), người này sẽ rút ra từ quỹ hưu của mình mỗi tháng là $2,000, trong vòng 20 năm (sau 20 năm thì vừa vặn hết quỹ hưu). Giả sử rằng mức lãi suất mà người này nhận được cho quỹ hưu của mình là cố định bằng lãi kép 5% hàng tháng. Hỏi giá trị của quỹ hưu vào thời điểm người này về hưu là bao nhiêu, và người này phải nộp hàng tháng bao nhiêu tiền vào quỹ hưu ? |
Giải:
Khi đó giá trị tương lai của niên kim tăng là:
$F=\dfrac{(1+i)^n-1}{i}\times R \Rightarrow R=F \times \dfrac{i}{(1+i)^n-1}$
Giá trị hiện tại của niên kim giảm:
$P=\dfrac{1-(1+i)^n}{i}\times 2000 $ 

Ta biết rằng giá trị tương lai $F$ của niên kim tăng bằng giá trị hiện tại $P$ của niên kim giảm. Do đó:


Như vậy, chỉ cần nộp $\$364.13$ một tháng cho quỹ hưu trong vòng 30 năm, thì có thể
nhận được lương hưu $\$2000$ một tháng trong vòng 20 năm, nếu lãi suất kép theo tháng
là 5%/năm.
Xem phần 2: THỰC HÀNH GIẢI QUYẾT BÀI TOÁN TÀI CHÍNH: NIÊN KIM (DÀNH CHO HS GIỎI) – P1
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay