Áp dụng của bài toán trả nợ dần - đề thi thử chuyên Vinh 2019

Ví dụ: Đề thi thử THPTQG 2019 Chuyên ĐH Vinh (lần 2).

Sau khi tốt nghiệp đại học, anh Nam thực hiện một dự án khởi nghiệp. Anh vay vốn từ ngân hàng 200 triệu đồng với lãi suất 0, 6% một tháng. Phương án trả nợ của anh Nam là: cuối mỗi tháng kể từ tháng đầu tiên anh bắt đầu trả nợ, hai lần trả nợ liên tiếp cách nhau đúng một tháng, số tiền trả của mỗi lần là như nhau và hoàn thành sau đúng 5 năm kể từ khi vay. Tuy nhiên, sau khi dự án có hiệu quả và đã trả nợ được 12 tháng theo phương án cũ anh Nam muốn rút ngắn thời gian trả nợ nên từ tháng tiếp theo, mỗi tháng anh trả nợ cho ngân hàng 9 triệu đồng. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi sau ít nhất bao nhiêu tháng từ thời điểm vay anh Nam trả hết nợ ? 

Ghi chú: Chúng tôi có điều chỉnh lại đề bài cho phù hợp với chủ đề đang thảo luận (đề gốc với phương án trả nợ là vào đầu mỗi tháng chúng ta sẽ bàn sau).

Giải:

Theo phương án ban đầu số tiền hàng tháng anh Nam phải nộp vào ngân hàng là:

$$200M(1+0.6\%)^{60}=\dfrac{R}{0.6\%}((1+0.6\%)^{60}-1)$$

(ký hiệu kỹ thuật trong máy tính Casio fx580VNX, 1M=10^6), $1M$ đọc là một mega.

Ra lệnh giải phương trình

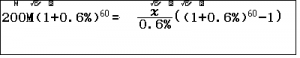
ta có $R$ bằng

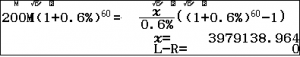
Vậy số dư nợ tại ngân hàng của anh Nam sau khi thanh toán xóng 12 tháng đầu tiên thep phương án  ban đầu là:

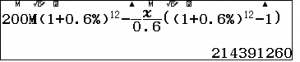
Do đó thời gian còn lại để trả hết nợ theo phương án tiếp theo  là:

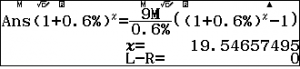
Vậy để trả hết nợ theo giai hai đoạn anh Nam cần một thời gian là $12+20=32$ tháng, rút ngắn 28 tháng so với dự kiến ban đầu.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.