Viết nhanh phương trình đường thẳng đi qua A và cắt hai cả hai đường thẳng d1,d2

Trong không gian với hệ trục toạ độ Đê-cac vuông góc $\large Oxyz$ cho điểm $\large A(1;2;3)$ và hai đường thẳng

$\large d_1: \frac{x}{2}=\frac{y+1}{-2}=\frac{z-2}{1}; d_2: \left\{\begin{matrix} x=4t & \\ y=-2 & \\ z=3t & \end{matrix}\right.$

Viết phương trình đường thẳng đi qua $\large A$ và cắt cả hai đường thẳng $\large d_1,d_2$

Giải.

Đường thẳng cần tìm là giao tuyến của hai mặt phẳng

• $\bullet$ $\large \text{mp}(A,d_1)$ với cặp vectơ chỉ phương là $\large \vec{a}=(2;-2;1);\overrightarrow{BA}= (1;3;1)$
• $\bullet$ $\large \text{mp}(A,d_2)$ với cặp vectơ chỉ phương là $\large \vec{b}=(4;0;3);\overrightarrow{CA}= (1;4;3)$

Vectơ chỉ phương của đường thẳng cần tìm là $\large (\vec{a}\times \overrightarrow{BA})\times (\vec{b} \times\overrightarrow{CA})$

w513 nhập VctA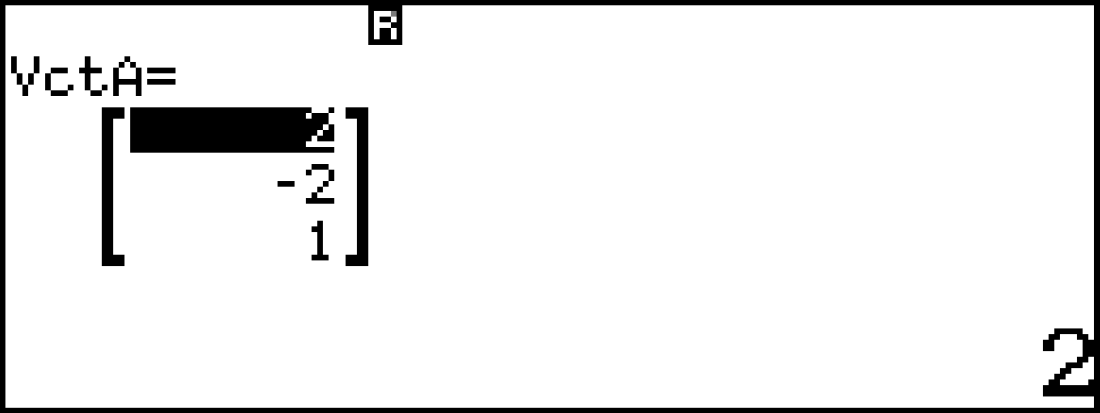

T123 nhập VctB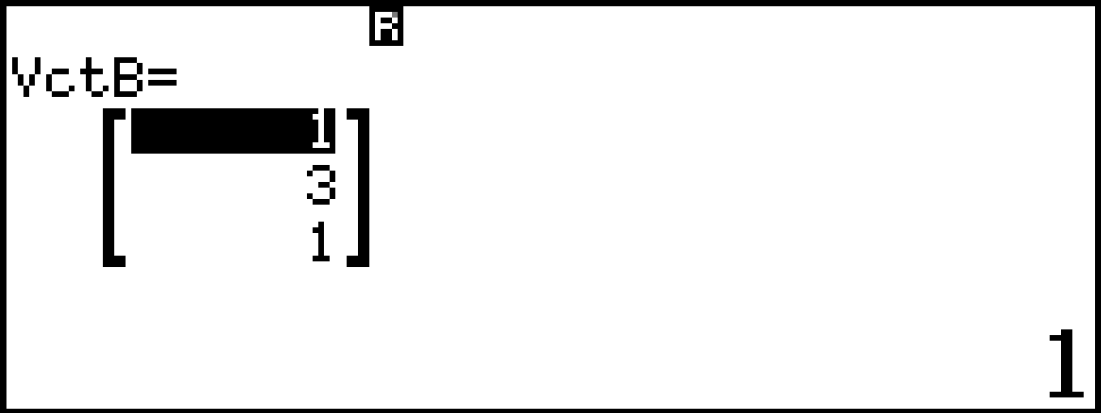

T133 nhập VctC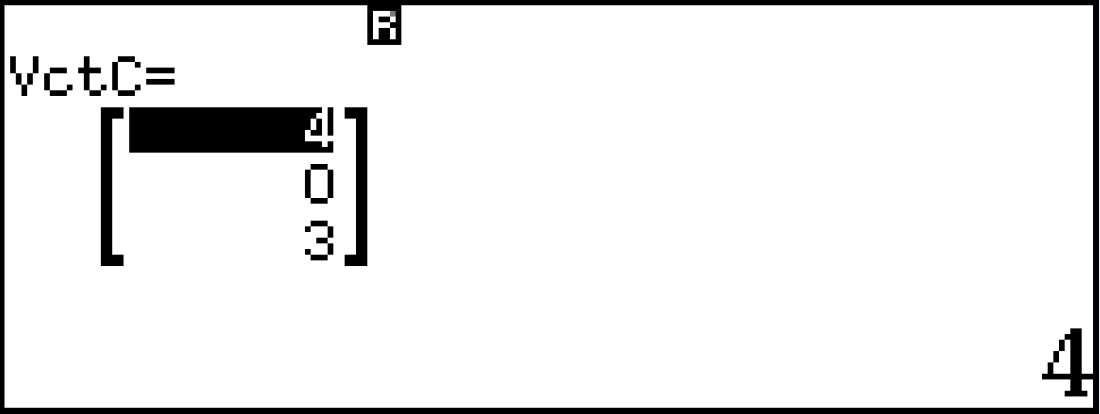

T143 nhập VctD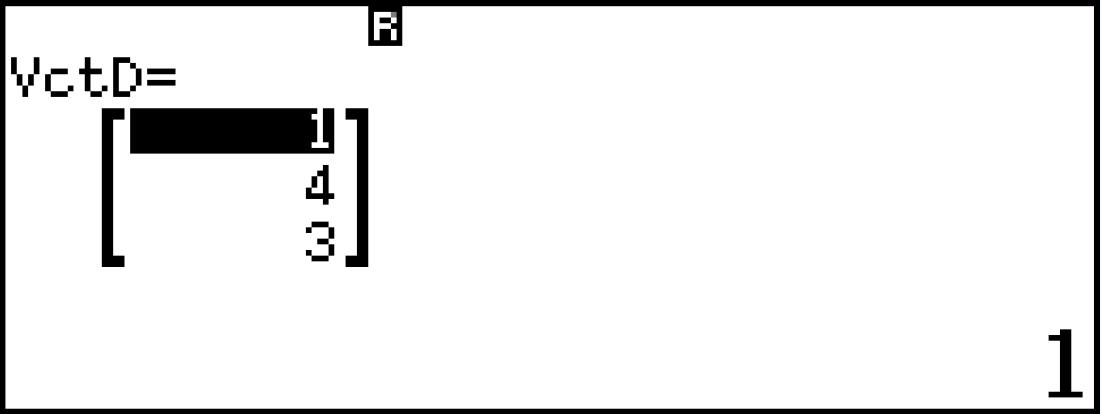

C

Đáp số: $$\large \frac{x-1}{56}=\frac{y-2}{-16}=\frac{z-3}{33}$$

About Bitex_PTGD

Đam mê toán học. Quản trị viên Diễn Đàn Toán Casio. Mọi thắc mắc, quý thầy cô và các bạn học sinh vui lòng liên hệ vào hộp thư Inbox tại Fanpage: Diễn Đàn Toán Casio.