BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
5 chữ số cuối cùng của số $5^{2015}$.
- 29/11/2021
- 514 lượt xem
| Bài toán: Tìm 5 chữ số cuối cùng của số $5^{2015}$. |
Đây từng là bài toán rất khó đối với học sinh và ngay cả một số giáo viên phụ trách đội tuyển.
Chúng tôi gợi ý cách giải như sau:
Trước hết ta nhận biết số
| $$2015=\displaystyle\sum_{n=1}^{4}2^n+\sum_{n=6}^{10}2^n+1.$$ |
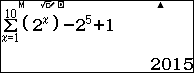
Vậy $$5^{2015}=\underbrace{5^{2^1}\times5^{2^2}\times5^{2^3}\times5^{2^4}\times5^{2^6}\times5^{2^7}\times5^{2^8}\times5^{2^{10}}}_{\large \text{số sau là bình phương của số trước, không kể số } 5^{2^6}}\times 5^1$$
Thao tác trên máy tính, kết hợp ghi ra giấy (sẽ nhanh hơn lưu vào các biến nhớ).
Lần đầu:
.
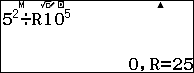Các lần sau đều dùng:
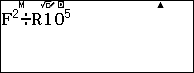
Ta có:
$5^{2^1}\equiv 25\ \text{mod}\ 10^5$
$5^{2^2}\equiv 625\ \text{mod}\ 10^5$
$5^{2^3}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^4}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^6}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^7}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^8}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^9}\equiv 90625\ \text{mod}\ 10^5$
$5^{2^{10}}\equiv 90625\ \text{mod}\ 10^5$
$5^{1}\equiv 5\ \text{mod}\ 10^5$
Nhận xét: 
Ta có: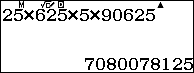 
| Vậy 5 chữ số cuối cùng của số $5^{2015}$ là $78125$. |
Gợi ý:
| Tìm 5 chữ số cuối cùng của số $23^{2022}$ |
Hướng dẫn: 
Đáp số: $\ 41329$
About TS. Nguyễn Thái Sơn
