Sử dụng máy tính casio giải bài toán Malfatti
- 11/10/2019
- 584 lượt xem
Bài toán: Cho tam giác $ABC$. Bên trong tam giác này hãy vẽ ba đường tròn tiếp xúc nhau và mỗi cái tiếp xúc với hai cạnh của tam giác $ABC$.

Đây là bài toán nổi tiếng do nhà toán học Ý Malfatti (1731-1807) đặt ra vào năm 1803 và đã được giải trong tập 10 của Memorie di Matematica e di Fisica della Società italiana delle Scienze. Lời giải khá hàn lâm và đòi hỏi nhiều công cụ vẽ hình nếu chỉ vẽ bằng thước kẻ và compa.(Ví dụ hãy vẽ một góc mà sin bình phương của góc đó bằng một số cho trước).
Trong bài viết này chúng tôi nêu ra đáp án và dùng máy tính Casio fx-580 VNX dể tính toán và tiến hành vẽ hình. Lưu ý các bạn, một bài toán vẽ hình là một bài toán hàn lâm và chỉ được vẽ bằng thước và compa.
Tuy nhiên do độ phức tạp của lời giải chúng tôi chọn phương pháp tính toán gần đúng với sai số 10 số không sau dấu phẩy thập phân.
Đáp án:
- Gọi $p$ là nửa chu vi tam giác $ABC$ và đặt $a=\dfrac{BC}{p}, b=\dfrac{CA}{p}, c =\dfrac{AB}{p}$. Điều này có nghĩa là, không làm mất tính tổng quát, ta giả sử tam giác $ABC$ có nửa chu vi bằng đơn vị.
- Tính
$\alpha=\dfrac{\arcsin(\sqrt{a})+\arcsin(\sqrt{b})+\arcsin(\sqrt{c})}{2}- \arcsin(\sqrt{a})$.$\beta=\dfrac{\arcsin(\sqrt{a})+\arcsin(\sqrt{b})+\arcsin(\sqrt{c})}{2}- \arcsin(\sqrt{b})$.$\gamma=\dfrac{\arcsin(\sqrt{a})+\arcsin(\sqrt{b})+\arcsin(\sqrt{c})}{2}- \arcsin(\sqrt{c})$. - Đặt $u=p.\sin^2(\alpha), v=p.\sin^2(\beta), w=p.\sin^2(\gamma)$.
Dựng hình:
- Dùng $A$ làm tâm vẽ một đường tròn bán kính $u$, cắt $AB$ tại $V$. Qua $V$ dựng đường thẳng vuông góc với $AB$ cắt đường phân giác trong góc $A$ tại $I$. Dùng $I$ làm tâm vẽ đường tròn đi qua $V$ ta có đường tròn thứ nhất.
- Dùng $B$ làm tâm vẽ một đường tròn bán kính $v$, cắt $BC$ tại $T$. Qua $T$ dựng đường thẳng vuông góc với $BC$ cắt đường phân giác trong góc $B$ tại $J$. Dùng $J$ làm tâm vẽ đường tròn đi qua $T$ ta có đường tròn thứ hai.
- Dùng $C$ làm tâm vẽ một đường tròn bán kính $w$, cắt $BC$ tại $Q$. Qua $Q$ dựng đường thẳng vuông góc với $BC$ cắt đường phân giác trong góc $C$ tại $K$. Dùng $K$ làm tâm vẽ đường tròn đi qua $Q$ ta có đường tròn thứ ba.
Thực hành trên máy tính Casio
Giả sử ta xét tam giác $ABC$ với kích thước như sau:
$BC=10.66, CA=10.63, AB=6.19$
$a=$ 
$b=$ 
$c =$ 




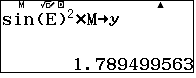



 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay