BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI MỘT SỐ BÀI TOÁN THỰC TẾ HÌNH HỌC TRONG CT THCS 2019-2020
- 06/12/2019
- 1,437 lượt xem
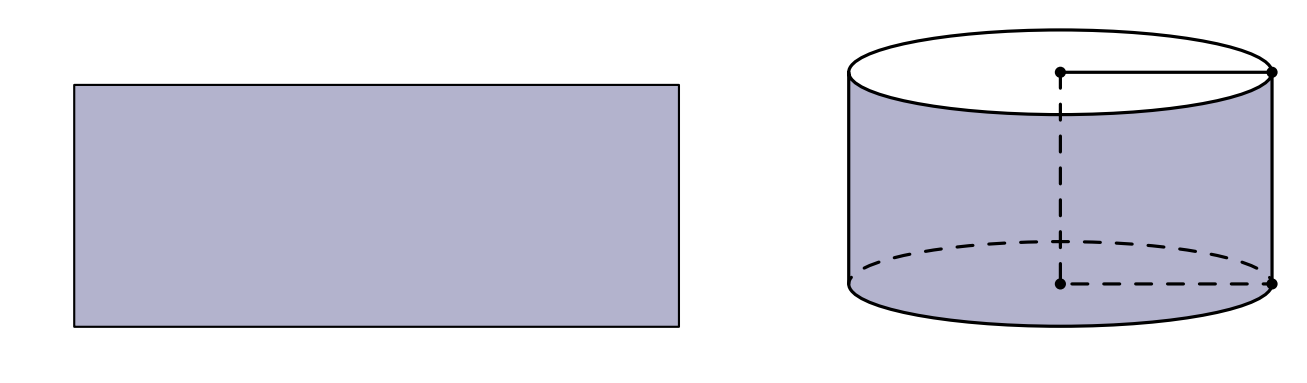
Câu 1. Từ một tấm tôn hình chữ nhật có kích thước $0{,}5\text{ cm}\times 2\text{ cm}$ người ta gò tấm tôn đó thành mặt xung quanh của thùng đựng nước hình trụ có chiều cao bằng $0{,}5$ m (phần mép không đáng kể). Tính thể tích $V$ của thùng
|
A. $V=\dfrac{1}{\pi}$ (m$^3$). |
B. $V=\dfrac{5}{2\pi}$ (m$^3$). |
|
C. $V=\dfrac{2}{\pi}$ (m$^3$). |
D. $V=\dfrac{1}{2\pi}$ (m$^3$). |
Hướng dẫn
Hình trụ được tạo thành có chiều cao $h=0{,}5$ m. Chu vi đường tròn đáy bán kính $r$ chính bằng chiều dài của hình chữ nhật ban đầu, nên ta có $2\pi r=2\Rightarrow r=\dfrac{1}{\pi}$.
Vậy thể tích của thùng là $V=B\cdot h=0{,}5\cdot \pi r^2=\dfrac{1}{2\pi}$ (m$^3$).
Chọn câu D.
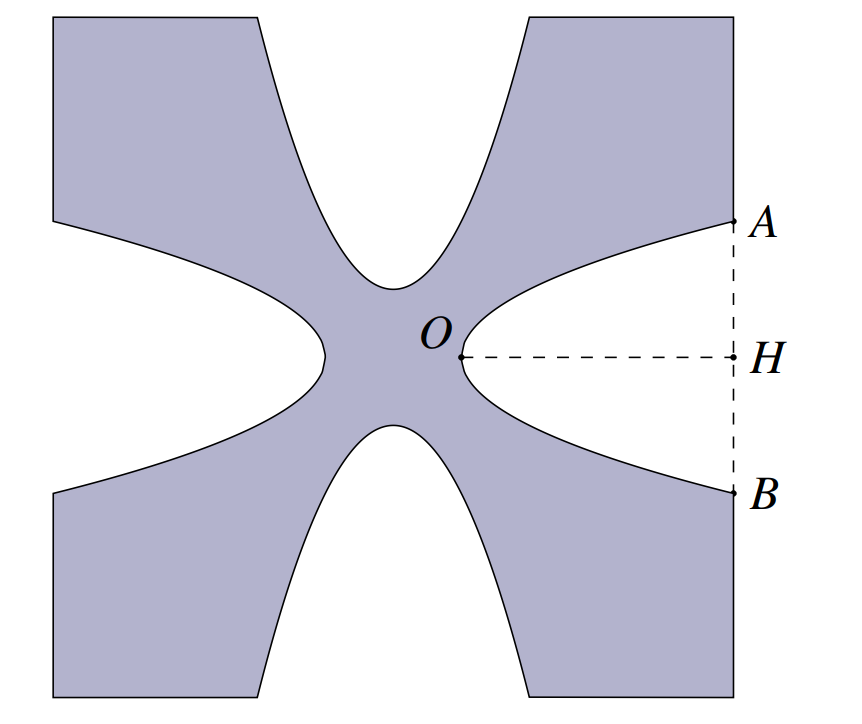
Câu 2. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh $10$ cm, bằng cách lần lượt khoét đi bốn phần bằng nhau có hình dạng parabol như hình vẽ bên. Biết $AB = 5$ cm, $OH = 4$ cm và diện tích phần gạch sọc được tính theo công thức $S =\dfrac{4}{3} HA \cdot OH$. Tính diện tích bề mặt hoa văn đó (phần hình được tô đen).
|
A. $\dfrac{160}{3}\ \mathrm{cm^2}$. |
B. $\dfrac{140}{3}\ \mathrm{cm^2}$. |
|
C. $\dfrac{14}{3}\ \mathrm{cm^2}$. |
D. $50\ \mathrm{cm^2}$. |
Hướng dẫn
Diện tích của phần tô đen là $10^2 – \dfrac{16}{3} HA \cdot OH = \dfrac{140}{3}\ \mathrm{cm^2}$.
About Bitex Khánh Vũ
