VỀ BÀI TOÁN HÌNH HỌC TRONG BÀI THI HSG (THPT) MÁY TÍNH CASIO

Trong bài thi HSG máy tính cầm tay chỉ có một bài toán hình học. Bài toán hình học đó dựa vào các tỉ lệ giữa hai đoạn thẳng trong tam giác. Cụ thể như sau:

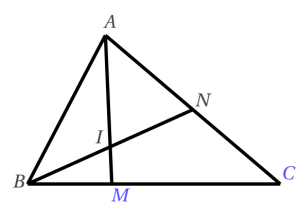
Trong mặt phẳng cho tam giác $ABC$. Trên đoạn BC ta ta lấy điểm $M$ sao cho $\dfrac{BM}{BC}=m$, trên đoạn $AC$ ta lấy điểm $N$ sao cho $\dfrac{AN}{AC}=n$. Hai đường thẳng $AM$ và $BN$ cắt nhau tại $I$.

Tính $\dfrac{AI}{AM}$ và $\dfrac{BI}{BN}$.

Bài giải

Thay vì tính $\dfrac{AI}{AM}$ ta tính tỉ số của hai vectơ $\overrightarrow{AI}$ và $\overrightarrow{AM}$. Để tính tỉ số vectơ ta có thể dùng hệ toạ độ afin trong mặt phẳng.

Chọn mục tiêu afin gốc B $\{B; C, A\}$. Khi đó ta có toạ độ afin của các điểm:

$B(0;0), C(1;0), A(0;1), M(m;0), N(n;1-n)$ (chú ý phương trình đường thẳng $AC$ là $x+y=1$.)

Phương trình đường thẳng AM là $\dfrac{x}{m}+y=1$, $BN: y=\dfrac{1-n}{n}$

Giải hệ phương trình trên tìm được toạ độ giao điểm $I$ là $I\left(\dfrac{mn}{m+n-mn};\dfrac{m-mn}{m+n-mn}\right)$.

Toạ độ vectơ $\overrightarrow{AI}=\left(\dfrac{mn}{m+n-mn};\dfrac{-n}{m+n-mn}\right)$.

$\overrightarrow{AM}=(m;-1)$

Vậy tỉ số của hai vectơ $\overrightarrow{AI}$ và $\overrightarrow{AM}$ là $$\dfrac{n}{m+n-mn}$$

Suy ra (ghi nhớ) $\dfrac{AI}{AM}=\dfrac{n}{m+n-mn}$

Tương tự: $\dfrac{BI}{BN}=\dfrac{m}{m+n-mn}$.

Áp dụng: Cho tam giác $ABC$ với kích thước $AB=3,5, BC=5,3, CA=4,8$. Gọi $M$ là trung điểm $AC$, $N$ trên đoạn $BC$ sao cho $BC=3BN.$ $BM$ cắt $AN$ tại $I$. Tính $IA, IB,IC$. Sau đó tính các đoạn $SA, SB, SC$ với $S$ là đỉnh của khối tứ diện $SABC$ và $SI=7$ là đường cao của khối tứ diện.

Giải: Chú ý vai trò của chữ $M$ và chữ $N$ bị hoán vị với phần giáo khoa trình bày ở trên.

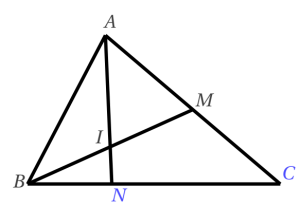
Ta có: $\dfrac{AI}{AN}=\dfrac{n}{m+n-mn}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{6}}=\dfrac34$

$\dfrac{BI}{BM}=\dfrac{m}{m+n-mn}=\dfrac{\dfrac{1}{3}}{\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{6}}=\dfrac12$

• Ta tính $AN^2$
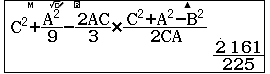
  $AN$ , suy ra $IA$ Vậy $SA=$ 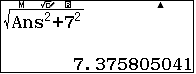$\approx 7,38$
• Ta tính $BM^2$
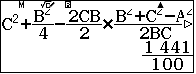
  $BM$ $BI$
  Vậy $SB=$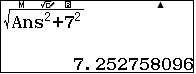$\approx 7,25$
• Lưu ý ta đã lưu $IB$ vào D.
  Ta tính $IC^2=$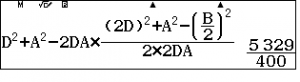
  $IC=$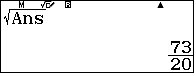 Vậy $SC=$$\approx 7,89$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.