BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
HỆ THỨC LƯỢNG TRONG TAM GIÁC (TIẾP THEO)
- 04/12/2019
- 1,688 lượt xem
Nhắc lại bài toán:
Cho tam giác $ABC$ có cạnh $AB=5.7 ; BC=8.3, CA=7.6$. Đường trung tuyến $AM$ cắt phân giác $BD$ tại $I$. Tính (chính xác đến 2 chữ số thập phân):
a) Bán kính $R$ của đường tròn ngoại tiếp tam giác $CDM$.
c) Bán kính $r$ của đường tròn nội tiếp tam giác $CDM$.
d) Diện tích S của tứ giác $CDIM$.
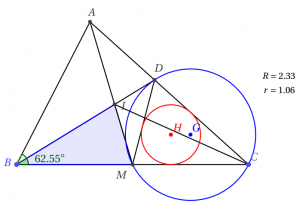
Ta tính đoạn phân giác $BD=$ 
Suy ra $MD=$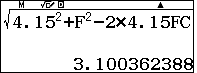
lưu vào biến nhớ E.
1. Diện tích tam giác khi biết ba cạnh.
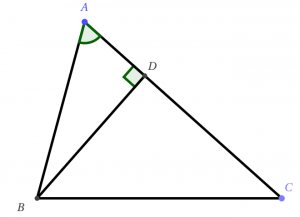Hạ đường cao BD.
$S_{ABC}=\dfrac12.AC.BD$
mà $BD=AB.\sin A$ nên
$$S_{ABC}=\dfrac12.AB.AC.\sin A$$
2. Bán kính đường tròn ngoại tiếp
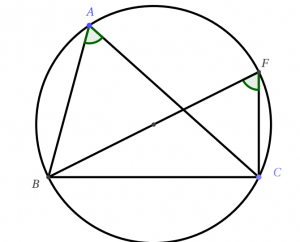
$\sin A=\dfrac{BC}{2R}\Leftrightarrow R=\dfrac{BC}{2\sin A }$
3. Bán kính đường tròn nội tiếp
Ta ghi nhận công thức sau đây:
$$r=\dfrac{2S_{ABC}}{AB+BC+CA}$$
việc chứng mnh công thức dành cho GV phụ trách đội tuyển.
GIẢI BÀI TOÁN
Để có bài học độc lập, trong bài tập này chúng ta nhập liệu lại từ đầu, qui ước$$BC=a, CA=b, AB=c$$
1. Bán kính $R$ của đường tròn ngoại tiếp tam giác $CDM$.
Ta tính các cạnh của tam giác CDM
- Cạnh $DM$.
Tính $\dfrac12 \widehat{B}=$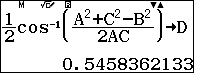
Độ dài đường phân giác trong $BD=$: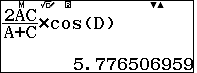
Vậy $DM=$
- Tính góc $\widehat{C}$
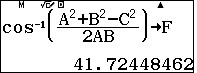
- Bán kính $R$ của đường tròn ngoại tiếp tam giác $CDM$ bằng
$\approx 2,33$
2. Bán kính $r$ của đường tròn nội tiếp tam giác $CDM$.
$$r=\dfrac{2S_{CDM}}{CD+DM+MC}=\dfrac{2\times \dfrac12\times CD.CM.\sin C}{CD+DM+CM}$$
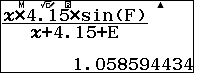$\approx 1,06$
3. Diện tích tứ giác $CDIM$.
Tính lại $BI=$
suy ra $CI=$
$S_{CDIM}=S_{CID}+S_{CIM}$
About TS. Nguyễn Thái Sơn
