BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Định lý VI-ET cho phương trình bậc 2, bậc 3,... bậc n
- 10/01/2022
- 4,831 lượt xem
Trong toán học, định lý Viète hay công thức Viète (có khi viết theo phiên âm tiếng Việt là Vi-ét) do nhà toán học Pháp Francois Viète tìm ra, nêu lên mối quan hệ giữa các nghiệm của một phương trình đa thức (trong trường số phức) và các hệ số của nó.
1. Phương trình bậc hai
Nếu ${x_1}$ và ${x_2}$ là hai nghiệm của phương trình: $\mathbf{a{x^2}+bx+c=0, a\ne{0}}$
thì: $\left\{ \begin{array}{l}\mathbf{{x_1}+{x_2}=S=-\dfrac{b}{a}\\{x_1}{x_2}=P=\dfrac{c}{a}}\end{array} \right.$
2. Phương trình bậc ba
Nếu ${x_1}$,${x_2}$ và ${x_3}$ là ba nghiệm của phương trình: $\mathbf{a{x^3}+b{x^2}+cx+d=0, a\ne{0}}$
thì: $\left\{ \begin{array}{l}\mathbf{{x_1}+{x_2}+{x_3}=-\dfrac{b}{a}\\{x_1}{x_2}+{x_2}{x_3}+{x_3}{x_1}=\dfrac{c}{a}\\{x_1}{x_2}{x_3}=-\dfrac{d}{a}}\end{array} \right.$
3. Phương trình đa thức bất kỳ
Nếu ${x_1}$,${x_2}$,…,${x_n}$ là $n$ nghiệm của phương trình: $\mathbf{{a_n}{x^n}+{a_{(n-1)}}{x^{(n-1)}}+ … +{a_2}{x^2}+{a_1}x+{a_0}=0, {a_n}\ne{0}}$
thì: $\left\{ \begin{array}{l}\mathbf{a={a_n}\\-a({x_1}+{x_2}+…+{x_n}={a_{(n-1)}}\\…\\…\\{(-1)^{(n-1)}}a({x_1}{x_2}…{x_{(n-1)}}+{x_1}{x_2}…{x_{(n-2)}}{x_n}+…+{x_2}{x_3}…{x_n})={a_1}\\{(-1)^n}a({x_1}{x_2}…{x_n})={a_0}}\end{array} \right.$
4. Áp dụng
Bài toán 1: Không giải phương trình $\mathbf{{x^2}-5x+6=0}$ $(1)$
Tính giá trị của biểu thức: $\mathbf{P=\dfrac{2({x_1}+{x_2})}{{x_1}{x_2}}+\dfrac{2{x_1}{x_2}}{{x_1}+{x_2}}}$ khi ${x_1}$ và ${x_2}$ là hai nghiệm của phương trình $(1)$
Áp dụng định lý Vi-ét, ta có:
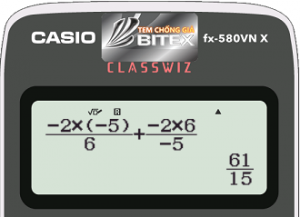
$P=\dfrac{2({x_1}+{x_2})}{{x_1}{x_2}}+\dfrac{2{x_1}{x_2}}{{x_1}+{x_2}}$
$=\dfrac{-2b}{c}+\dfrac{-2c}{b}$
$=\dfrac{61}{15}$
Các bạn có góp ý hay bình luận gì cho bài viết này hay muốn ad viết về vấn đề nào thì đừng ngại để lại bình luận hoặc gửi tin nhắn trên fanpage cho ad nhá.
About Toanbitexdtgd1
