MTCT trợ giúp giải hệ phương trình khó (THCS) - Bài 1

Đề thi vào lớp 10 SGD và ĐT Nghệ An năm học 2021-2022

 
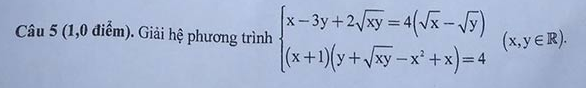
Điều kiện $x\geqslant 0\ ; y \geqslant 0$. Đặt $u=\sqrt{x}, v=\sqrt{y}$, phương trình thứ nhất trở thành
$$u^2+2(v-2)u-3v^2+4v=0$$

$\Delta’=4(v-1)^2$.

Vậy $\left[\begin{array}{l}u=-v+2+2(v-1)=v\\ u=-v+2-2(v-1)=-3v+4\end{array}\right.$
 

1. 1. Nếu $u=v$ thay vào phương trình còn lại ta được
   $$(u^2+1)(-u^4+3u^2)=4\Leftrightarrow -(u^2)^3+2(u^2)^2+3u^2-4=0\Leftrightarrow -x^3+2x^2+3x-4=0$$
   Bấm MTCT giải phương trình bậc ba, chỉ nhận nghiệm không âm,

   

   hai nghiệm thập phân lưu vào A và B

   

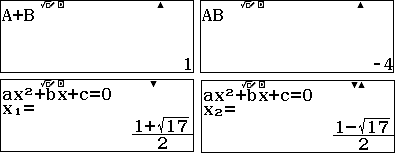
   Trong trường hợp này hệ có hai nghiệm $$\left\lbrace\begin{array}{l}x=1\\ y=1\end{array}\right.\qquad ; \qquad \left\lbrace\begin{array}{l}x=\dfrac{1+\sqrt{17}}{2}\\ y=\dfrac{1+\sqrt{17}}{2}\end{array}\right.$$

2. 2. Nếu $u=-3v+4$ thay vào phương trình còn lại ta được
   $$(u^2+1)\Big[\left(\dfrac{u-4}{-3}\right)^2+u\left(\dfrac{u-4}{-3}\right)-u^4+u^2\Big]=4$$
   $$\Leftrightarrow (u^2+1)\Big[u^2-8u+16-3u(u-4)-9u^4+9u^2\Big]=36$$
   • $\color{blue}\bullet$ Viết lên màn hình:
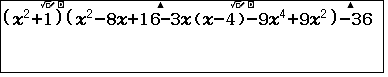
   • $\color{blue}\bullet$ Bấm SHIFT SOLVE với giá trị nhập vào $x=0$
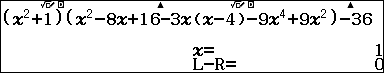
   • $\color{blue}\bullet$ Biểu thức chia hết cho $x-1$ và hệ số tạo thành không vượt quá 50 nên bấm CALC100 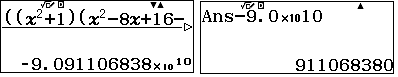đổi dấu, chuyển thành
      
     $9|09|11|06|83|80\rightarrow 9x^5+9x^4+11x^3+7x^2-16x-20$
   • $\color{blue}\bullet $ Bấm SHIFT SOLVE phương trình tạo thành
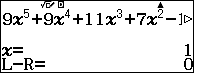
   • $\color{blue}\bullet$ Đa thức chia hết cho $x-1$ và hệ số tạo thành không vượt quá 50 nên bấm CALC 100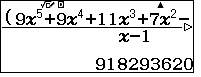. Thương của phép chia là đa thức bậc 4 $9x^4+18x^3+29x^2+36x+20$.

     Đa thức bậc 4 này vô nghiệm

   

    

   Về phương diện trình bày lời giải học sinh chỉ cần viết $\qquad (u^2+1)\Big[u^2-8u+16-3u(u-4)-9u^4+9u^2\Big]=36$ $\qquad \Leftrightarrow (u-1)^2(9u^4+18u^3+29u^2+36u+20)=0$ $\qquad \Leftrightarrow (u-1)^2\Big[(3u^2+3u)^2+20\left(u+\dfrac{9}{10}\right)^2+\dfrac{19}{5}\Big]=0 \Leftrightarrow u=1$.

    
   Vậy trong trường hợp này ta có $u=1, v=1$, do đó hệ có một nghiệm $x=y=1$.

 
Tóm lại hệ đã cho có hai nghiệm
$$\left\lbrace\begin{array}{l}x=1\\ y=1\end{array}\right.\qquad ; \qquad \left\lbrace\begin{array}{l}x=\dfrac{1+\sqrt{17}}{2}\\ y=\dfrac{1+\sqrt{17}}{2}\end{array}\right.$$

 
còn tiếp.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.