BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
THỰC HÀNH TRÊN CASIO FX 9860GII SD - BÀI TOÁN TRẢ NỢ DẦN
- 09/07/2019
- 829 lượt xem
| Bài 1: Một khoản vay $\$5000$ được trả dần hàng tháng vào cuối mỗi tháng trong hai năm với lãi kép 7% hàng tháng. Tìm số dư nợ sau 8 tháng. |
Chú ý: lãi kép 7% hàng tháng, nghĩa là lãi kép $\dfrac{7\%}{12}$/tháng với kỳ hạn 1 tháng.
Giải: Bằng phương pháp tính toán truyền thống
Ta có công thức: $$P_n=P(1+i)^n-\dfrac{R}{i}\Big[(1+i)^n-1\Big]$$
Số tiền trả hàng tháng của khoản vay trả nợ dần này bằng:
$R=\dfrac{P(1+i)^{24}\times I}{(1+i)^{24}-1}=\dfrac{5000\left(1+\dfrac{7\%}{12}\right)^{24}\times 7\%}{\left(1+\dfrac{7\%}{12}\right)^{24}-1}\approx 223.8628955$
Vậy số dư nợ sau 8 tháng trả dần là:
$$P_8=P(1+i)^8-\dfrac{R}{i}\Big[(1+i)^8-1\Big]=\$3410.256063$$
Sau đây ta sử dung tính năng TVM của máy tính Casio fx-9860 GII SD.
Bước 1: Tính tô ($R$) (tiền trả hàng tháng của bài toán trả nợ dần)
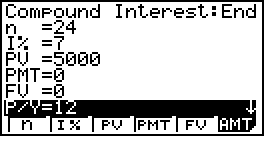
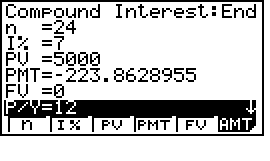
Bước 2: Bấm F6 để chuyển màn hình sang AMT (Amortization)
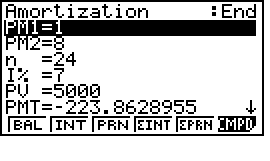chọn PM1=1 và PM2=8 (từ kỳ hạn trả dần đầu tiên đến kỳ hạn trả dần thứ 8), sau đó bấm F1 (BAL) (Balance, số dư nợ):
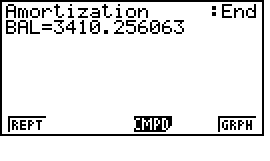
| Bài 2: Một khoản vay $\$5000$ được trả dần hàng tháng vào cuối mỗi tháng trong hai năm với lãi kép 7% hàng tháng. Tìm tiền lãi và tiền nạp vào nợ gốc (để làm giảm nợ gốc) của lần thanh toán thứ 9. |
Giải:
Cài đặt máy tính như trên.
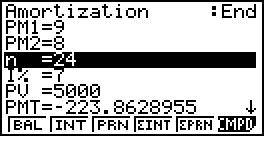Lưu ý PM1=9, PM2 tuỳ ý khác 0.
Bấm F2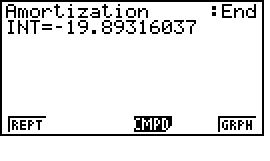 
. Đây là tiền lãi (Interest) mà người cho vay được hưởng trong lần thanh toán thứ 9.
Bấm F1 để trở lại và bấm F3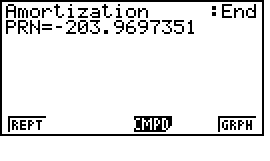 
để tính phần nạp vào nợ gốc.
Tiền tô của mỗi kỳ thanh toán được chia ra làm hai phần: phần lãi và phần nộp vào nợ gốc để làm giảm dư nợ. Các bạn có thể tham khảo thêm bảng tính sau đây:
Loading...
Reload document 
Open in new tab
Bảng tính được thực hiện trên LibreOffice Calc.
- Tô (B4) được tính bằng công thức:
$$=PMT(B1/12,B2,-B3)$$ - Số dư nợ tính theo công thức: $$P(1+i)^n-\dfrac{R}{i}((1+i)^n-1)$$
- Lãi bằng lãi suất nhân cho dư nợ của kỳ thanh toán trước
- Nạp vào nợ gốc bằng tô trừ đi lãi.
| Bài 3: Một khoản $\$35,000$ được vay để mua một chiếc xe hơi. Khoản vay này sẽ trả dần hàng tháng vào cuối mỗi tháng trong ba năm với lãi kép 3% hàng tháng. Tìm tổng số tiền lãi trong 12 lần thanh toán của năm thứ hai . |
Giải:
Bước 1: Tính tô
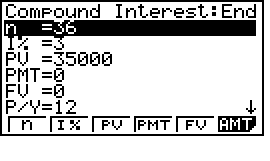
Bước 2: Bấm F1 để trở ra và bấm F6 để vào AMO
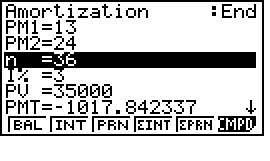nhập PM1=13 và PM2=24
sau đó bấm F4 sẽ tìm được tổng tiền lãi trong 12 lần thanh toán của năm thứ hai
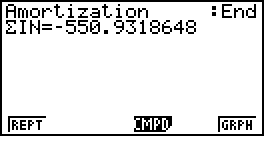
Dấu $-$(âm), nghĩa là đây là số tiền lãi người vay nộp vào cho ngân hàng, quỹ tín dụng hoặc người cho vay.
About TS. Nguyễn Thái Sơn
