ỨNG DỤNG KIẾN THỨC ĐẠI SỐ TRONG CÁC BÀI TOÁN THỰC TẾ THCS
- 23/05/2022
- 887 lượt xem
Trong bài viết này, Diễn đàn muốn chia sẻ đến bạn đọc một vài bài toán thường gặp trong chương trình Toán THCS
Nguồn tham khảo SÁCH CHINH PHỤC CÁC DẠNG TOÁN THỰC TẾ THCS VỚI MÁY TÍNH CASIO FX-580VN X VÀ FX-570VN PLUS
Bài 1. Nhiệt độ sôi của nước không phải lúc nào cũng là $100^\circ{C}$ mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển ($x=0 (m)$) thì nước có nhiệt độ sôi là $y=100^o C$ nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao $x=3600m$ so với mực nước biển thì nhiệt độ sôi của nước là $87^o C$. Ở độ cao trong khoảng vài $km$ người ta thấy mối quan hệ giữa hai đại lượng này là một hàm số bậc nhất $y=ax+b$ có đồ thị như sau:

$x(m)$: là đại lượng biểu thị cho độ cao so với mực nước biển.
$y(^{\circ}C)$: là đại lượng biểu thị cho nhiệt độ của nước.
a/ Xác định các hệ số $a$ và $b$.
b/ Thành phố Đà Lạt có độ cao $1500m$ so với mực nước biển. Hỏi nhiệt độ sôi của nước ở thành phố này là bao nhiêu?
Hướng dẫn giải
a/ Xác định các hệ số $a$ và $b$.
Từ đồ thị ta có
$\begin {cases} 100=a.0+b\\ 87=a.3600+b\end {cases} \Longleftrightarrow\begin {cases}b=100\\a.3600+100=87 \end {cases} $
Sử dụng phương thức EQUATION để giải hệ phương trình:
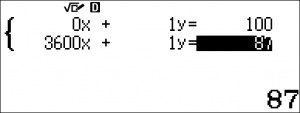



Vậy $a=-\dfrac{13}{3600} \approx -0,0036$ và $b=100$.
* Để tìm số gần đúng của a, ta lưu x vào biến nhớ A, sau đó sử dụng qb

b/ Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là $2,85$ atm?
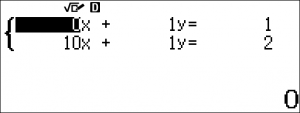


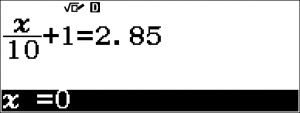
Mặt khác $y_1=\dfrac{x_1}{10}+1$\\
Do đó $\dfrac{x_1}{10}+1=2,85 \Longrightarrow x_1=18,5 (\text{m})$

Số sản phẩm $1$ người làm trong $1$ ngày là: $20:5=4$ (sản phẩm)
Thời gian $4$ người đến sau làm việc là: $10-4=6$ (ngày)
Trong $6$ ngày, $4$ người làm được số sản phẩm là: $4 \times 6 \times 4 = 96$ (sản phẩm)
Vậy trong $10$ ngày tổ công nhân sản xuất được số sản phẩm là: $200+96=296$ (sản phẩm)
- $x$ là số công nhân lúc đầu có ở phân xưởng $A$ ,
- $y$ là số công nhân lúc đầu có ở phân xưởng $B$ (Điều kiện $x,y \in \mathbb{N^*}$)
Như vậy ta có hệ phương trình
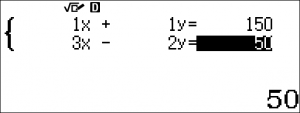
$\begin {cases}x + y = 150\\\dfrac{2}{3}(x – 10) = \dfrac{4}{9}(y + 10)\end{cases} $$ \Longleftrightarrow\begin {cases}x + y = 150\\6x – 60= 4y + 40\end{cases} $$ \Longleftrightarrow\begin {cases}x + y = 150\\3x – 2y = 50\end{cases}$
$\Longleftrightarrow\begin {cases}3x +3 y = 450\\3x – 2y = 50\end{cases} $$ \Longleftrightarrow\begin {cases}x + y = 450\\5y = 400\end{cases} $$ \Longleftrightarrow\begin {cases}x = 150 – y\\y = 80\end{cases}$$ \Longleftrightarrow\begin {cases}x = 70\\y = 80\end{cases}$


Trong một ngày theo kế hoạch tổ công nhân phải làm được $$140: (x -4) = \dfrac{140}{x – 4}\text{ (sản phẩm)}$$
Trong một ngày thực tế tổ công nhân làm được $140: x = \dfrac{140}{x}$ (sản phẩm)
Theo đầu bài ta có phương trình: $\dfrac{140}{x -4} – \dfrac{140}{x} = 4$
$\Longleftrightarrow\dfrac{35}{x -4} – \dfrac{35}{x} = 1$
$\Longleftrightarrow 35x – 35(x – 4) = x(x -1)$
$\Longleftrightarrow 35x – 35x + 140 = x^2 -4x$
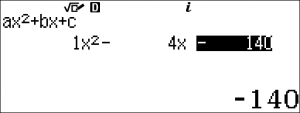
$\Longleftrightarrow x^2 -4x – 140 = 0$
Ta có $ \Delta ‘ = 4 + 140 = 144, \sqrt {\Delta ‘} = 12$
Suy ra $x_1 = \dfrac{2 + 12}{1} = 14$ (nhận) và $x _2 = \dfrac{2 – 12}{1} = -10 $ (loại)
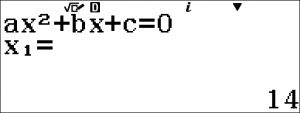
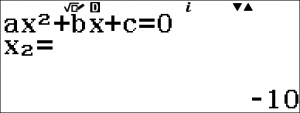
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay