BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI QUYẾT CÁC BÀI TOÁN THỰC TẾ BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH
- 25/02/2019
- 7,985 lượt xem
Toán thực tế là một nội dung rất hay, đa dạng và thường xuất hiện trong các đề thi tuyển sinh lớp 10. Tuy nhiên, học sinh thường gặp rất nhiều khó khăn trong việc giải quyết các bài toán này. Lập hệ phương trình là một trong những phương pháp phổ biến nhất được sử dụng để giải quyết các bài toán thực tế trong chương trình THCS. Dưới đây là một số bài toán minh họa :
Bài toán 1. Hai vòi nước cùng chảy vào bể thì sau 6 giờ đầy bể . Nếu mỗi vòi chảy một mình cho đầy bể thì vòi II cần nhiều thời gian hơn vòi I là 5 giờ. Tính thời gian mỗi vòi chảy một mình đầy bể?
Hướng dẫn giải bằng cách lập hệ phương trình
Gọi $latex x,y$ giờ ($latex x,y>0$ ) lần lượt là thời gian để vòi I và vòi II một mình chảy đầy bể
Trong một giờ thì vòi I chảy được $latex \dfrac{1}{x}$ (bể), vòi II chảy được $latex \dfrac{1}{y}$ (bể)
Do nếu hai vòi cùng chảy thì sau 6 giờ đầy bể nên ta có: $latex 6\left( \dfrac{1}{x}+\dfrac{1}{y} \right)=1\Leftrightarrow 6\left( x+y \right)=xy$
Ngoài ra theo đề bài ta có: $latex y-x=5$
Như vậy ta có hệ phương trình: $latex \left\{ \begin{align} & 6\left( x+y \right)=xy \\ & y-x=5 \\\end{align} \right.$$latex \Leftrightarrow \left\{ \begin{align} & 6\left( 5+2x \right)={{x}^{2}}+5x \\ & y=5+x \\\end{align} \right.$ $latex \Leftrightarrow \left\{ \begin{align} & {{x}^{2}}-7x-30=0 \\ & y=5+x \\\end{align} \right.$
Sử dụng máy tính Casio fx 580vnx để giải phương trình $latex {{x}^{2}}-7x-30=0$
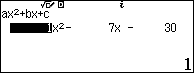
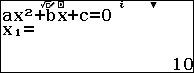
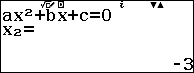
Do $latex x>0$ nên $latex x=10$ suy ra $latex y=5+x=15$
Vậy thời gian để vòi I và vòi II một mình chảy đầy bể lần lượt là $latex 10$ giờ và $latex 15$ giờ
Bài toán 2. Năm ngoái tổng dân số của hai tỉnh A và B là 4 triệu người. Dân số tỉnh A năm nay tăng $latex 1.2\%$, còn tỉnh B tăng $latex 1.1\%$ và tổng số dân của hai tỉnh năm nay là $latex 4045000$ người. Tính số dân của mỗi tỉnh năm ngoái và năm nay.
Hướng dẫn giải bằng cách lập hệ phương trình
Gọi $latex x,y$ ($latex x,y>0$) lần lượt là dân số của hai tỉnh A và B vào năm ngoái.
Biết rằng tổng dân số của hai tỉnh vào năm ngoái là 4 triệu người, suy ra: $latex x+y={{4.10}^{6}}$
Theo đề bài ta có:
Dân số tỉnh A năm nay là $latex 1.012x$
Dân số tỉnh B năm nay là $latex 1.011y$
Tổng số dân của hai tỉnh năm nay là $latex 1.012x+1.011y=4045000$
Như vậy ta có hệ phương trình: $latex \left\{ \begin{align} & x+y={{4.10}^{6}} \\ & 1.012x+1.011y=4045000 \\\end{align} \right.$
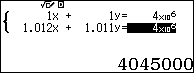
Vậy dân số của tỉnh A và B năm ngoái lần lượt là $latex 1$ triệu và $latex 3$ triệu người
Dân số của tỉnh A và B năm nay lần lượt là $latex 1012000$ người và $latex 3033000$ người
Bài toán 3. Có hai lọ dung dịch muối 1 và 2 với nồng độ lần lượt là $latex 5\%$ và $latex 20\%$. Người ta pha trộn hai dung dịch trên để có $latex 1kg$ dung dịch mới có nồng độ $latex 14\%$. Hỏi phải dùng bao nhiêu gam mỗi loại dung dịch? (biết $latex C\%=\dfrac{{{m}_{ct}}}{{{m}_{\text{dd}}}}.100\%$ , $latex C\%$: nồng độ phần trăm, $latex {{m}_{ct}}$: khối lượng chất tan và $latex {{m}_{\text{dd}}}$ : khối lượng dung dịch)
Hướng dẫn giải bằng cách lập hệ phương trình
Gọi $latex x,y$ (gam) lần lượt là khối lượng của dung dịch 1 và 2
Khối lượng chất tan trong 1 và 2 lần lượt là $latex 0.05x$(gam) và $latex 0.2y$(gam)
Sau khi pha trộn hai dung dịch trên ta có:
Tổng khối lượng dung dịch là $latex x+y=1000$
Tổng khối lượng chất tan là $latex 0.05x+0.2y=0.14\times 1000=140$
Như vậy ta có hệ phương trình $latex \left\{ \begin{align} & x+y=1000 \\ & 0.05x+0.2y=140 \\\end{align} \right.$
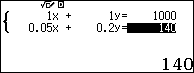
Vậy khối lượng dung dịch 1 và 2 lần lượt là $latex 400$gam và $latex 600$ gam
Bài toán 4. Bạn Bình tham gia luyện tập môn leo núi. Sau khi đi lên dôc và đến được đỉnh núi, Bình đi tiếp một phần đường bằng có chiều dài $latex 2.5$ km rồi đi xuống dôc đến một cái hồ. Sau đó, Bình đi theo chiều ngược lại và theo con đường cũ. Vận tốc khi đi trên đường bằng là $latex 5\left( km/h \right)$, khi lên dốc là $latex 4\left( km/h \right)$, lúc xuống dốc là $latex 6\left( km/h \right)$. Chiều đi bạn mất $latex 1$ giờ $latex 36$ phút, chiều về mất $latex 1$ giờ $latex 39$ phút. Hỏi chiều dài quãng đường từ vị trí xuất phát đến cái hồ là bao nhiêu km?
Hướng dẫn giải bằng cách lập hệ phương trình
Ta có: $latex 1$ giờ $latex 36$ phút $latex =1.6$ giờ; $latex 1$ giờ $latex 39$ phút$latex =1.65$giờ
Gọi $latex x$ (km) là chiều dài đoạn dốc lên lúc đi
$latex y$ (km) là chiều dài đoạn dốc xuống lúc đi
Theo đề bài ta có:
Thời gian lúc đi là: $latex \dfrac{x}{4}+\dfrac{2.5}{5}+\dfrac{y}{6}=1.6$ $latex \Leftrightarrow \dfrac{x}{4}+\dfrac{y}{6}=1.1$
Thời gian lúc về là: $latex \dfrac{x}{6}+\dfrac{2.5}{5}+\dfrac{y}{4}=1.65$$latex \Leftrightarrow \dfrac{x}{6}+\dfrac{y}{4}=1.15$
Vậy ta có hệ phương trình: $latex \left\{ \begin{align} & \dfrac{x}{4}+\dfrac{y}{6}=1.1 \\& \dfrac{x}{6}+\dfrac{y}{4}=1.15 \\\end{align} \right.$
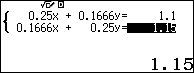
Vậy chiều dài quãng đường là: $latex x+2.5+y=9.9$ (km)
About Ngọc Hiền Bitex
