MỘT SỐ BÀI TOÁN VỀ ĐƯỜNG TRÒN NỘI TIẾP - NGOẠI TIẾP
- 06/05/2021
- 463 lượt xem
Bài 1: Cho có BC=8cm; AC=6cm; AB=7cm. Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp
.
Hướng dẫn:
Áp dụng công thức Herong ta có:
S
20.33
Sử dụng máy tính:
8Jz6Jx7JuaQz+Qx+QuR2=Jj
sQjO(QjpQz)O(QjpQx)O(QjpQu)=
Bài 2: Tính diện tích tam giác đều nội tiếp và ngoại tiếp đường tròn (O;R) với R=4,25 cm
Hướng dẫn:
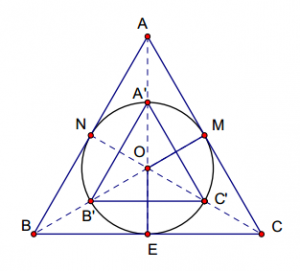
Gọi 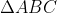 và
và 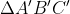 lần lượt ngoại tiếp và nội tiếp đường tròn (O; R)
lần lượt ngoại tiếp và nội tiếp đường tròn (O; R)
Trong 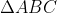 ba đường trung tuyến AE,BM và CN cắt nhau tại O
ba đường trung tuyến AE,BM và CN cắt nhau tại O
Sử dụng máy tính:


Bài 3: Cho tam giác ABC đều cạnh a=3,36 cm. Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác đều.
Hướng dẫn:
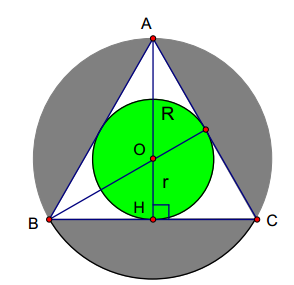
Gọi AH là đường cao hạ từ A xuống cạnh BC
Gọi O là giao của 3 đường trung tuyến trong tam giác đều, R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC;
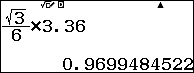
Sử dụng máy tính:

Bài 4: Cho tam giác ABC vuông tại A có AB=3cm, AC=4cm. Goi R là bán kính đường tròn ngoại tiếp; r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số 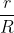 .
.
Hướng dẫn:
Tam giác ABC vuông tại A, nên 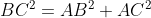 ( định lý Py-ta-go)
( định lý Py-ta-go)
Do đó bán kính đường tròn ngoại tiếp tam giác ABC là )
Diện tích tam giác ABC là S=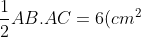)
Mặt khác ta có: 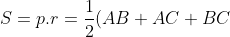.r)
Vậy tỉ số 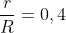
Bài 5: Tính diện tích hình bát giác đều nội tiếp đường tròn (O;8cm)
Hướng dẫn:
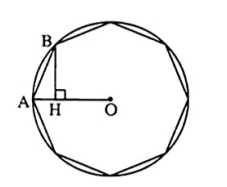
Gọi R là bán kính đường tròn ngoại tiếp hình bát giác đều thì R=8cm
Ta có: 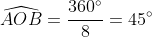
Gọi diện tích bát giác là S thì:
Chia sẻ
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay