BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
(LÝ THUYẾT) SỬ DỤNG CASIO FX 9860GII SD - GIẢI QUYẾT BÀI TOÁN TÀI CHÍNH 1
- 01/07/2019
- 553 lượt xem
1. Lãi tức, lãi suất và kỳ hạn
Khi ta mở một tài khoản tiết kiệm tại ngân hàng và gửi vào tài khoản đó một số tiền, ngân hàng sẽ trả cho ta một khoản để được quyền sử dụng số tiền đó, khoản này được gọi là lãi tức (interest) và được xác định bởi số tiền gửi, thời hạn gửi, và lãi suất.
Số tiền gửi này được gọi là giá trị gốc (principal value ) hoặc giá trị hiện tại (present value) và số tiền mà giá trị gốc tăng lên (sau khi cộng lãi tức vào giá trị gốc) được gọi là giá trị tương lai (future value) hoặc số dư (balance).
Trong tài liệu này, ví dụ khi ta nói lãi kép i(%) hàng quí (interest compounded quarterly) ta sẽ hiểu là:
lãi kép i(%) một năm với kỳ hạn là quí (3 tháng).
Ví dụ 1:
|
2. Giá trị hiện tại và giá trị tương lai.
| Công thức tính giá trị tương lai:$$F=(1+i)^nP$$ở đây $i$ là lãi suất tính theo kỳ hạn (dưới dạng số thập phân), $n$ là số kỳ hạn và $P$ là giá trị hiện tại. |
| Ví dụ 2: Tính số dư (balance) cho hai kỳ hạn đầu tiên của một khoản tiền gửi $1000 với lãi suất 2% bán niên. |
Giải: lãi suất 2% bán niên, nghĩa là lãi suất 2% một năm với kỳ hạn 6 tháng.
Vậy lãi suất cho một kỳ hạn là $\dfrac{2\%}{2}=0,01$
Áp dụng công thức
$$B_1=(1+0.01)^1\times 1000=1010$$
$$B_2=(1+0.01)^2\times 1000=1020,1$$
Vậy số dư sau kỳ hạn thứ nhất là $\$1010$ và sau kỳ hạn thứ hai là $\$1020,1$.
|
Ví dụ 3: Tính giá trị tương lai (future value) cho các kỳ hạn 5 năm và 10 năm của một khoản tiền gửi $100 với lãi suất tương ứng i% hàng quí. |
Giải:
Ta thực hiện tính trường hợp cụ thể với $i=10\%$, kỳ hạn $n=10$ năm = 40 (quí).
$\dfrac{10\%}{4}=0,025$
$(1+0,025)^{40}\times 100\approx 268,51$
Xem tất cả trường hợp trong bảng:
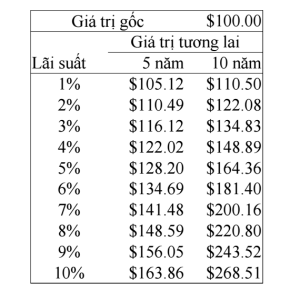
Lưu ý: Đây là bảng tính với dấu chấm thập phân thay vì dấu phẩy như chúng ta thường dùng.
3. Công thức tính giá trị gốc.
|
$$ P=\dfrac{F}{(1+i)^n}$$
|
|
Ví dụ 4: Cần phải gửi vào ngân hàng một khoản bao nhiêu để nhận được $1000 sau 5 năm với lãi kép 4% hàng quí. |
Giải: lãi kép 4% hàng quí, nghĩa là lãi kép 4% một năm, kỳ hạn 3 tháng.
Áp dụng công thức: $$F=P(1+i)^n \Leftrightarrow P=\dfrac{F}{(1+i)^n}$$
Vậy: $$P=\dfrac{100}{\left(
1+\dfrac{4\%}{4}\right) ^{20}}
\approx 819,5$$
Vậy cần phải gửi vào ngân hàng một khoản $819,5.
|
Ví dụ 5: Giả sử hôm nay là ngày 1/5/2019. Cần đầu tư một khoản bao nhiêu để nhận được $10.000 vào ngày 1/1/2028 nếu lãi kép 3% hàng tháng. |
Giải: lãi kép 3% hàng tháng nghĩa là lãi kép 3% một năm kỳ hạn một tháng.
Từ ngày 1/5/2019 đến 1/5/2028 có 9 năm tức là 108 tháng, từ ngày 1/1/2028 đến 1/5/2029 có 4 tháng. Vậy $n=104$ tháng.
Áp dụng công thức: $$P=\dfrac{10000}{\left(1+\dfrac{3\%}{12}\right)^{104}}\approx 7713,02$$
Như vậy $\$7713,02$ được đầu tư vào ngày 1/5/2019 sẽ nhân được $\ $10.000$ vào ngày 1/1/2028.
Bài tới: (THỰC HÀNH) BÀI TOÁN TÀI CHÍNH 1
About TS. Nguyễn Thái Sơn
