BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Vấn đề tìm khoảng cách từ điểm đến một mặt phẳng
- 26/01/2022
- 171 lượt xem
| Bài toán: Trong không gian cho hình chóp $SABC$ có đáy $ABC$ là tam giác vuông tại $A$, $SA\perp (BCD)$. Cho biết độ dài $AB, AC$ và $SA$. Tính khoảng cách từ $A$ đến mp$(SBC)$. |
| Hạ $AK\perp (SBC)$. Tứ diện $ASBC$ có các cạnh đi qua $A$ vuông góc với nhau từng đôi một nên $$\dfrac{1}{AK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}+\dfrac{1}{AS^2}$$
Kết luận: $d(A, (SBC)=\dfrac{1}{\sqrt{\dfrac{1}{AS^2}+\dfrac{1}{AB^2}+\dfrac{1}{AC^2}}}$ |
Áp dụng 1: Đề thi thử TN THPT 2021 môn Toán kênh truyền hình Giáo dục Quốc gia VTV7 (Đề 1)
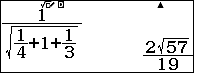
| Lưu ý: nếu không tinh ý phát hiện hình tính của khối tứ diện sẽ mất nhiều thời gian hơn để dựng hình và tính toán khoảng cách. |
Bây giờ ta sẽ xét trường hợp phức tạp hơn khi tam giác $ABC$ không có tính chất gì đặc biệt, giả sử đã biết ba cạnh của tam giác $ABC$.
| Hạ $AH\perp BC$. Mặt phẳng $(SBC)$ vuông góc với mặt phẳng $(SAH)$ và cắt mặt phẳng này theo giao tuyến $SH$. Hạ $AK\perp SH$ suy ra $AK$ vuông góc với mặt phẳng $(SBC)$.
$$\dfrac{1}{AK^2}=\dfrac{1}{AS^2}+\dfrac{1}{AH^2}$$ Ta có $AH.BC=AB.AC.\sin A\Rightarrow AH=\dfrac{AB.AC.\sin A}{BC}$ |
Vậy
| $$d(A,(SBC))=\dfrac{1}{ \sqrt{ \dfrac{BC^2}{AB^2.AC^2.\sin^2A}+\dfrac{1}{SA^2} } }$$ |
Áp dụng bằng số theo bài tập dưới đây.
Áp dụng 2: Đề thi THPTQG 2019
Vì $AB$ song song với $(SCD)$ nên $$d(B,(SCD))=d(A,(SCD))=\dfrac{1}{\sqrt{\dfrac{CD^2}{AD^2.AC^2.\sin^2\widehat{DAC}}+\dfrac{1}{SA^2}}}=\dfrac{1}{\sqrt{\dfrac{4}{AC^2}+\dfrac{1}{AS^2}}}$$
(vì $CD=DA$ và $\widehat{DAC}=30^\circ$)
Vậy $$d(B,(SCD))=\dfrac{1}{\sqrt{\dfrac{4}{DA^2+DC^2-2DA.DC.\cos 120^\circ}+\dfrac{1}{AS^2}}}$$
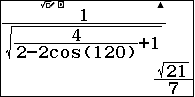
PS. Công thức $d(A,(SBC))=\dfrac{1}{
\sqrt{
\dfrac{BC^2}{AB^2.AC^2\sin^2A}+\dfrac{1}{SA^2}
}
}$ cũng sử dụng cho trường hợp tam giác vuông, xem như không phân biệt tam giác đáy, tuy nhiên yêu cầu cơ bản bắt buộc là $SA\perp (ABC)$.
About TS. Nguyễn Thái Sơn
