BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
THỦ THUẬT GIẢI NHANH CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN BẰNG MÁY TÍNH CASIO fx-580VN X
- 22/04/2021
- 3,170 lượt xem
Bài 1: Tìm m để khoảng cách từ A(1;2;3) đến mặt phẳng (P): x+3y+4z+m=0 bằng
Hướng dẫn:
Ta có:
Sử dụng máy tính:
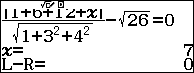
Như vậy ta thu được kết quả m=7
Bài 2: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Tính khoảng cách từ điểm M(-2;1;-1) tới d.
Hướng dẫn:
Đường thẳng d có vecto chỉ phương (1;2;-2) và đi qua điểm N(1;2;-2) có khoảng cách từ M đến d tính theo công thức:
với
và
Sử dụng máy tính:
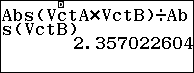
Vậy d(M;d)=2.357
Bài 3: Trong không gian Oxyz, tam giác ABC vuông tại A, , đường thẳng BC có phương trình
, đường thẳng AB nằm trong mặt phẳng (
) :x+z-3=0. Biết rằng đỉnh C có cao độ âm. Tìm hoành độ của đỉnh A.
Hướng dẫn:
Ta có B là giao điểm của đường thẳng BC và mặt phẳng .
Sử dụng máy tính:
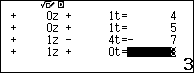
Như vậy B( 2;3;1)
C(4+t;5+t;-7-4t). Vì
nên t>
BC=
Từ đó suy ra t=-1. Vậy C(3;4;-3).
Sử dụng máy tính ta tính được góc giữa BC và là
Theo giả thiết góc giữa BC và AB cũng là nên A là hình chiếu vuông góc xủa C trên
.
Khi đó phương trình đường thẳng qua C và vuông góc với () là d và
.
Sử dụng máy tính để tính hoành độ điểm A
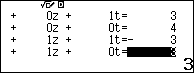
Bài 4: Trong không gian Oxyz, cho đường thẳng d có phương trình và 2 điểm A(-1;3;1), B(0;2;-1). Gọi C(m;n;p) là điểm thuộc d sao cho diện tích tam giác ABC bằng
. Tính giá trị của tổng m+n+p .
Hướng dẫn:
Xét hai vecto và
thì
Sử dụng máy tính:
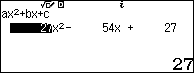
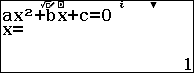
Như vậy t=1 thì m+m+p=2t+1=3
Bài 5: Trong không gian Oxyz, cho hai mặt phẳng (P); x-3y+2x-1=0 và (Q): x-z+2=0. Mặt phẳng () vuông góc với cả (P) và (Q) đồng thồi cắt trục Ox tại điểm có hoành độ bằng 3. Viết phương trình (
).
Hướng dẫn:
Sử dụng máy tính:
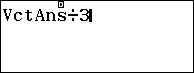
Như vậy () qua điểm (3;0;0) và vecto
nên phương trình (
) là: x+y+z-3=0.
About Bitex Khánh Vũ
