BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Về một câu vận dụng cao
- 24/07/2020
- 118 lượt xem
Trong đề thi thử chuyên Lam Sơn kỳ thi ngày 21/6/2020 có cho bài toán như sau:
Cho hàm số $y=\dfrac{bx+c}{dx^2+ex+f}$ với $\Delta = e^2-4df<0$
Khi đó cho biết đồ thị hàm số sẽ có ba điểm uốn thẳng hàng. Hãy viết phương trình đường thẳng đi qua 3 điểm này.
Lưu ý: Điểm uốn là điểm có hoành độ $x_0$ nằm trên đồ thị sao cho $y”(x_0)=0$.
Thực tế chỉ cho các hàm số với hệ số hằng số. Tuy nhiên ở đây để xây dựng công thức (học thuộc lòng) chúng tôi trình bày lời giải chính thống cho bài toán tổng quát này như sau
Ta có:
- $y’=\dfrac{Ax^2+Bx+C}{(dx^2+ex+f)^2}$ với $A=-bd; B= -2cd; C=bf-ec$
- $y”=-2 \dfrac{d(Ax^3+3Bx^2+3Cx)+eC-fB}{(dx^2+ex+f)^3}$
- $y”=0 \Leftrightarrow d(Ax^3+3Bx^2+3Cx)+eC-fB=0$
Chia đa thức bậc ba (VT) cho $dx^2+ex+f$ ta có thương là $Ax+be-3dc$ và dư là $-\Delta(bx+c)$
- Vậy $d(Ax^3+3Bx^2+3Cx)+eC-fB=(Ax+be-3dc)(dx^2+ex+f)+-\Delta(bx+c)$
- Suy ra phương trình đường thẳng đi qua ba điểm uốn là
$$Ax+be-3dc-\Delta y=0\Leftrightarrow {\color{blue}{bdx+\Delta y +3dc-be=0}}$$
Bài thi trắc nghiệm không thể cho một bài toán như thế, nhưng nếu là câu 50 và giảm độ khó của hàm đã cho, cách nhanh nhất là học thuộc công thức màu xanh ở trên. Câu 50 bài thi thử chuyên Lam Sơn là một câu giảm thiểu độ khó như thế và nếu vô tình học thuộc công thức thì may mắn đã đến với thí sinh :).
Sau đây chúng tôi gợi ý một câu ở mức độ vận dụng và giải trên máy tính Casio fx-580 VNX như sau:
Cho hàm số $y=\dfrac{x+1}{x^2+1}$. Biết rằng trên đồ thị có 3 điểm thẳng hàng sao cho đạo hàm cấp hai tại hoành độ của ba điểm đó đều bằng 0. Viết phương trình đường thẳng đi qua ba điểm nói trên. |
GIẢI
Ta chỉ cần tìm hai điểm rồi viết phương trình đường thẳng đi qua hai điểm.
- NHập phương trình $y”=0$ lên màn hình (nhớ lưu màn hình)
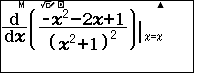
- Bấm SHIFT SOLVE hai lần tìm hai nghiệm lần lượt lưu vào A và B.
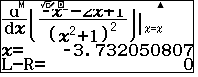
- Tính giá trị tương ứng lần lượt lưu vào C và D.
- Tính hệ số góc và tung độ gốc của đường thẳng
- Vậy phương trình đường thẳng cần tìm $y=\dfrac14x+\dfrac34$
About TS. Nguyễn Thái Sơn
