BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải câu 39 đề thi minh hoạ 2021
- 31/05/2021
- 195 lượt xem
Bài toán này thuộc dạng tìm GTLN, GTNN hoặc cực trị của hàm hợp $y=f(g(x))$ khi cho biết đồ thị hoặc bảng biến thiên của hàm số $y=f'(x)$. Đây cũng là bài toán hay gặp trong kỳ thi THPT của các năm qua.
Giải:
Đặt $t=2x$, bài toán trở thành tìm GTLN của hàm số $g(t)=f(t)-2t$ trên đoạn $[-3;4]$.
Ta có $g'(t)=f'(t)-2$
$g'(t)=0 \Leftrightarrow f'(t)=2$. Quan sát đồ thị:
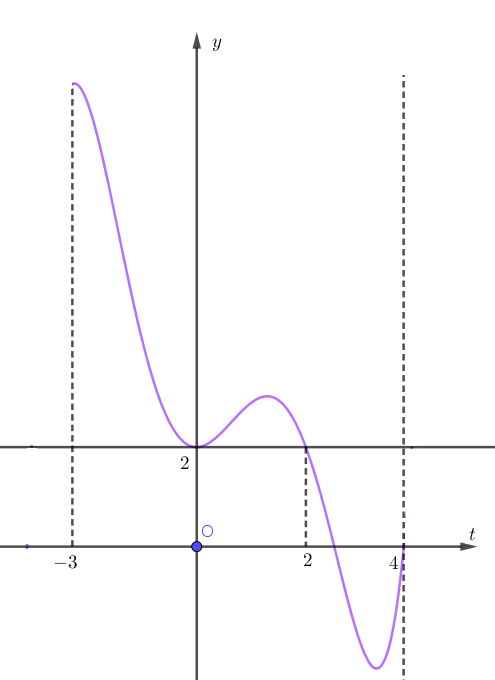
Ta có đồ thị của hàm số $y=f'(t)$ (trích lại đồ thị của hàm số đã cho đổi biến $t=2x$) và đường thẳng $y=2$ cắt nhau tại hai điểm có hành độ $t=0$ và $t=2$. Ta lập BBT của hàm số $y=g(t)$
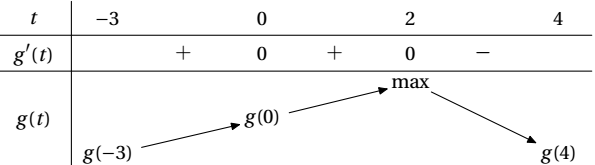
Giải thích bảng biến thiên.
Ta có $g'(t)=f'(t)-2$.
Bên trái và bên phải tại lân cận của điểm $(0;2)$, đồ thị $f'(t)$ (đường cong màu xanh) nằm trên đường thẳng $y=2$ nên tại hai phía giá trị $t=0$ đạo hàm đều dương.Bên trái tại lân cận của điểm $(2;2)$, đồ thị $f'(t)$ (đường cong màu xanh) nằm trên đường thẳng $y=2$ nên tại bên trái giá trị $t=2$ đạo hàm dương.
Bên phải tại lân cận của điểm có hoành độ $(2;2)$, đồ thị $f'(t)$ (đường cong màu xanh) nằm dưới đường thẳng $y=2$ nên tại bên phải giá trị $t=2$ đạo hàm âm.
Nhìn vào BBT của hàm số $g(t)$ trên đoạn $[-3;4]$ ta thấy GTLN của hàm $g(x)=f(2x)-4x=f(t)-2t$ là $g(2)=f(2)-4$, ta chọn C.
About TS. Nguyễn Thái Sơn
