Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bậc ba.
- 26/04/2022
- 825 lượt xem
Phương pháp:
Phương trình đường thẳng đi qua 2 điểm cực trị của hàm số $y=ax^3+bx^2+cx+d$ có dạng: $g(x)=y-\dfrac{y’.y”}{3y^{”’}}$.
+ Bước 1: Bấmw2để chuyển chế độ máy tính sang môi trường số phức.
+ Bước 2: Nhập vào máy tính biểu thức: $y-\dfrac{y’.y”}{3y^{”’}}$.
+ Bước 3: Bấm =để lưu biểu thức.
+ Bước 4: Bấmr với $x=i$ (đơn vị số phức, để làm xuất hiện $i$ ta bấmb).
+ Bước 5: Nhận kết quả dạng $Mi+N$. Phương trình cần tìm có dạng $y=Mx+N$.
Ví dụ 1: Phương trình đường thẳng đi qua hai điểm cực trị của hàm số $y=-2x^3+3x^2+1$ là
| A. $y=x-1$ | B. $y=x+1$ | C. $y=-x+1$ | D. $y=-x-1$ |
Lời giải
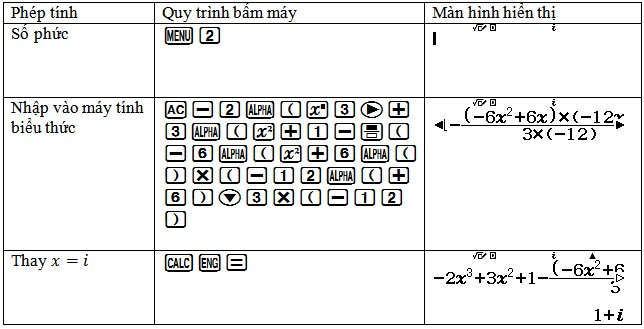
Kết quả dạng $1+i$, phương trình cần tìm là $y=x+1$. Chọn B.
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay