VỀ BÀI TOÁN HÌNH HỌC KHÔNG GIAN TRONG BÀI THI HSG (THPT) MÁY TÍNH CASIO

Cho một khối tứ diện $SABC$ biết kích thước của sáu cạnh, tìm thể tích và bán kính mặt cầu ngoại tiếp khối tứ diện đó. 

1. Thể tích của khối tứ diện $SABC$.Giả sử các kích thước như sau: $AB=c, BC=a, CA=b; SA=\alpha, SB=\beta, SC=\gamma$ 

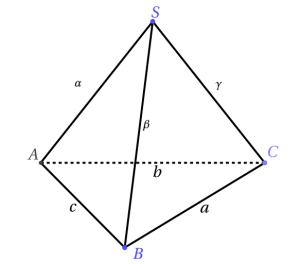Công thức: $$V=\dfrac{1}{12}\sqrt{A+B+C-D}$$

(để dễ nhớ, không sợ nhầm lẫn giữa kích thước với tên các đỉnh).$A, B, C, D$ được tính như sau:

• Tính tổng bình phương của sáu cạnh lưu vào F.
• $A=a^2\alpha^2(F^2-2(a^2+\alpha^2))$
• $B=b^2\beta^2(F^2-2(b^2+\beta^2))$
• $C=c^2\gamma^2(F^2-2(c^2+\gamma^2))$
• $D=a^2b^2c^2+a^2\beta^2\gamma^2+b^2\alpha^2\gamma^2+c^2\alpha^2\beta^2$

2. Bán kính mặt cầu ngoại tiếp khối tứ diện.

$$R=\dfrac{S}{6V}$$

trong đó $V$ là thể tích khối tứ diện, $S$ là “diện tích” (tính theo công thức Hê-rông) của một tam giác có các cạnh là tích của các cặp cạnh đối diện ($a\alpha, b\beta, c\gamma$) của khối tứ diện.

Ví dụ: Cho khối tứ diện $SABC$ với các kích thước sau đây:

$AB=3,5, BC= 5,3, CA=4,8$,

$SA=7,375805041, SB=7,252758096, SC=7,894460083$.

1. Tính chiều  cao $BK$ của khối tứ diện.
2. Tính bán kính mặt cầu ngoại tiếp khối tứ diện.

Giải

1. Tính chiều  cao $BK$ của khối tứ diện.

Trước hết ta tính thể tích khối tứ diện trên máy Casio fx-580VN X

Nhập 6 cạnh vào máy tính:

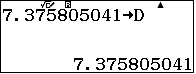
Tính số liệu trung gian để tìm thể tích khối tứ diện

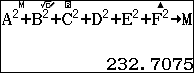
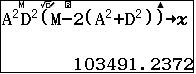
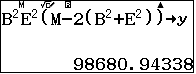
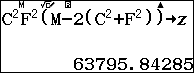
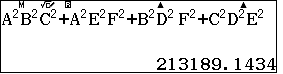
Thể tích khối tứ diện $SABC$

Để tìm chiều  cao $BK$ của khối tứ diện ta áp dụng công thức.

$$BK=\dfrac{3V}{S_{SAC}}$$

trong đó $S_{SAC}$ tính theo công thức Hê-rông với ba cạnh $AC \rightarrow $ B, $SA \rightarrow $ D, $SC \rightarrow $ F,

Khi  

Khi đó $BK=$ $\approx 3,32$

2. Tính bán kính mặt cầu ngoại tiếp khối tứ diện.

Áp dụng công thức $R=\dfrac{S}{6V}$

trong đó $S$ là diện tích tính theo công thức Hê-rông của một tam giác có các cạnh là tích của các cặp cạnh đối diện của khối tứ diện.

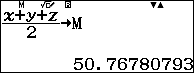
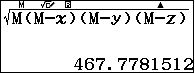
Vậy bán kính của mặt cầu ngoại tiếp khối tứ diện $SABC$ là

$\approx 4,07$

About TS. Nguyễn Thái Sơn

nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). Giảng viên thỉnh giảng ĐHSP TP HCM.