BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG TABLE TÌM GTLN, GTNN CỦA MỘT MỘT BIỂU THỨC CHO TRƯỚC
- 14/12/2021
- 1,512 lượt xem
Ví dụ : Câu 36 Đề Thi Thử -Sở Giáo Dục Đào Tạo Bắc Ninh – năm học 2017-2018
Cho hai số $x, y$ thỏa mãn $log (x + 2y) = \log x + \log y$. Khi đó, giá trị nhỏ nhất của biểu thức $P = \dfrac{{{x^2}}}{{1 + 2y}} + \dfrac{{4{y^2}}}{{1 + x}}$ là
$A. 6$ $B.\dfrac{32}{5}$ $C.\dfrac{31}{5}$ $D.\dfrac{29}{5}$
Giải
Từ $\log (x + 2y) = \log x + \log y \Rightarrow x + 2y = xy \Rightarrow y = \dfrac{x}{{x – 2}}$
Ta được: $P = \dfrac{{{x^2}}}{{1 + 2y}} + \dfrac{{4{y^2}}}{{1 + x}} = \dfrac{{{x^2}}}{{1 + \dfrac{{2x}}{{x – 2}}}} + \dfrac{{4{{\left( {\dfrac{x}{{x – 2}}} \right)}^2}}}{{1 + x}}$
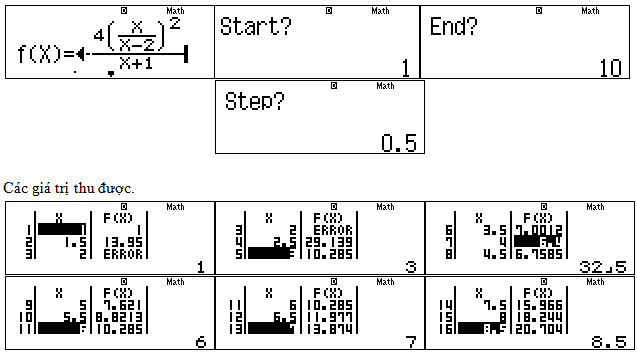
Ta vào mode 7 ( TABLE) để dự đoán giá trị nhỏ nhất thuộc khoảng nào.
Ta nhận thấy tại khoảng $\left( {3,5;4,5} \right)$ . Tại đó P đổi chiều vậy giá trị nhỏ nhất phải nằm trong khoảng đó. Vậy ta có thể kết luận ${P_{\min }} = \dfrac{{32}}{5}$
tại $x=4$. ( Có thể chia nhỏ hơn trong đoạn 3,5 đến 4,5 để hoàn toàn tin tưởng giá trị đã chọn). Chọn đáp án B.
About toancasiobitex
