Ứng dụng Casio fx 580vnx Tìm nhanh nguyên hàm của hàm số
- 28/11/2018
- 1,525 lượt xem
Ví dụ Tìm nguyên hàm của hàm số [latex]\large y=f(x)=\frac{1}{x^3+x^5}[/latex]
A. [latex]\large F(x)=\frac{1}{2x^2}-ln|x|+\frac{1}{2}ln(1+x^2)+C[/latex]
B. [latex]\large F(x)=-\frac{1}{2x^2}-ln|x|+\frac{1}{2}ln(1+x^2)+C[/latex]
C. [latex]\large F(x)=-\frac{1}{2x^2}-ln|x|-\frac{1}{2}ln(1+x^2)+C[/latex]
D. [latex]\large F(x)=-\frac{1}{2x^2}+ln|x|+\frac{1}{2}ln(1+x^2)+C[/latex]
w8 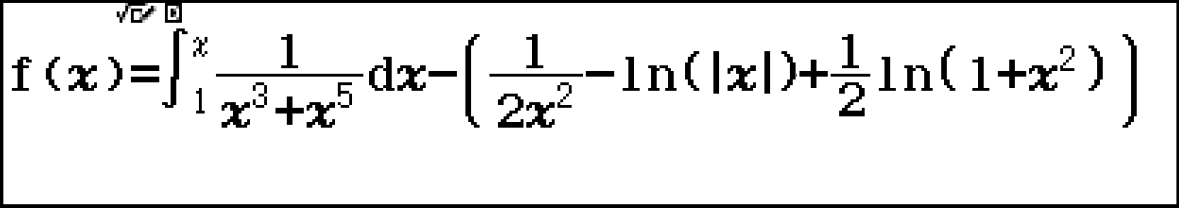
w8 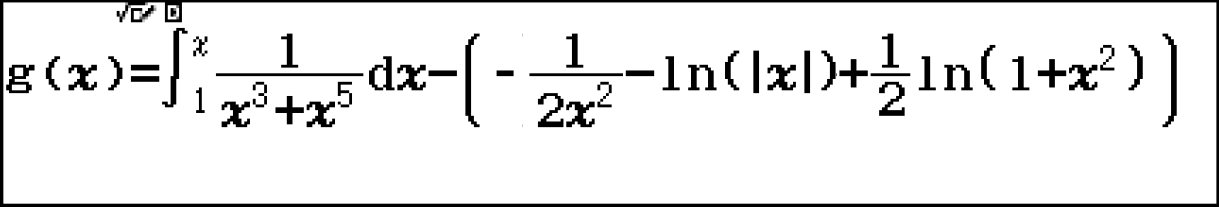

Cách thực hiện này mang ý nghĩa sư phạm nhiều hơn là mang ý nghĩa về việc tính toán. Vì máy tính phải tính 60 tích phân nên thời gian thực hiện chậm.
Duyệt bảng ta thấy [latex]\large g(x)[/latex] là hằng số, điều này phù hợp với định nghĩa nguyên hàm:
Vậy phương án đúng là B.
Nếu bỏ qua yếu tố sư phạm, chỉ quan tâm tới việc nhanh chóng biết kết quả, ta sẽ thực hiện theo phương pháp truyền thống như sau:
1. Lấy một số ngẫu nhiên lưu vào A.
2. Thử phương án A. 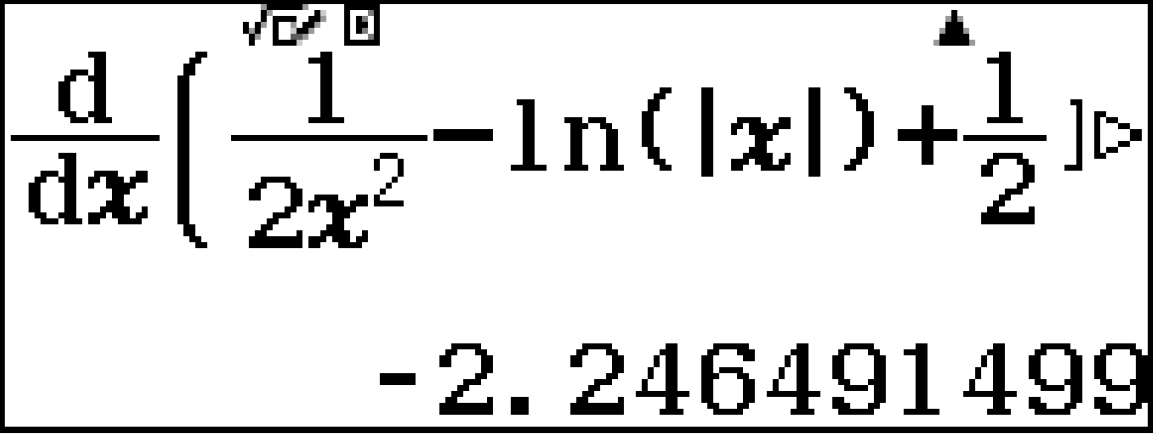
3. Thử phương án B. 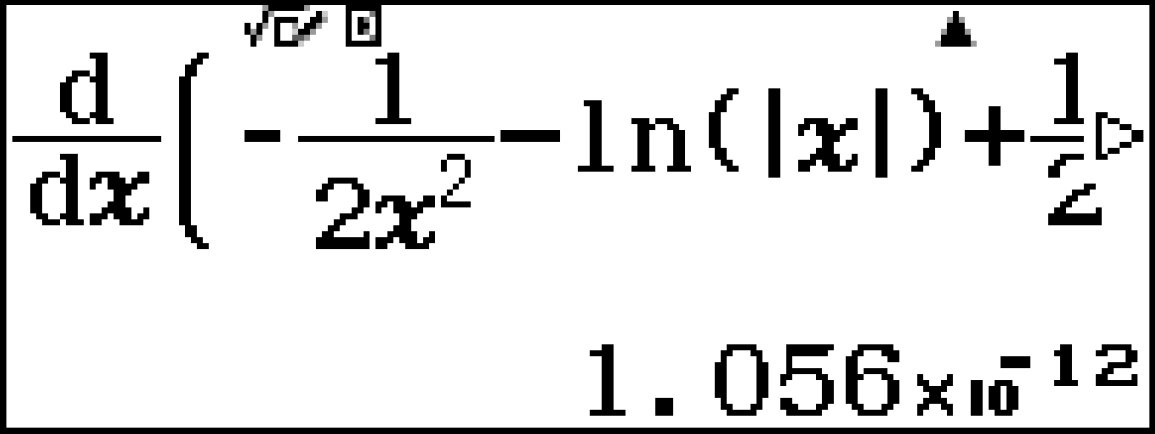 [latex]\large \approx 0[/latex] (đúng). Vậy chọn B.
[latex]\large \approx 0[/latex] (đúng). Vậy chọn B.
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay