BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Viết nhanh đường thẳng đi qua 2 điểm cực trị trên máy tính CASIO fx-580VN X
- 03/08/2018
- 5,191 lượt xem
Bài toán: Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số: $y=x^3-2x^2-x+1$.
Lời giải
Cách 1: Tìm cụ thể các điểm cực trị:
Tính ${y}’=3{{x}^{2}}-4x-1$ . $y’ = 0 \Leftrightarrow 3{x^2} – 4x – 1 = 0 \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2 + \sqrt 7 }}{3}\\ x = \dfrac{{2 – \sqrt 7 }}{3} \end{array} \right.$.
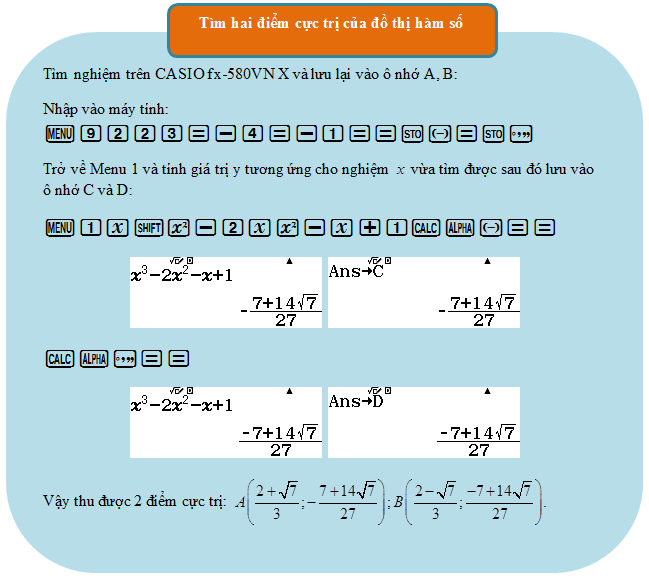
Có được hai điểm cực trị, dùng Menu Equation để tìm nhanh đường thẳng đi qua hai điểm cực trị
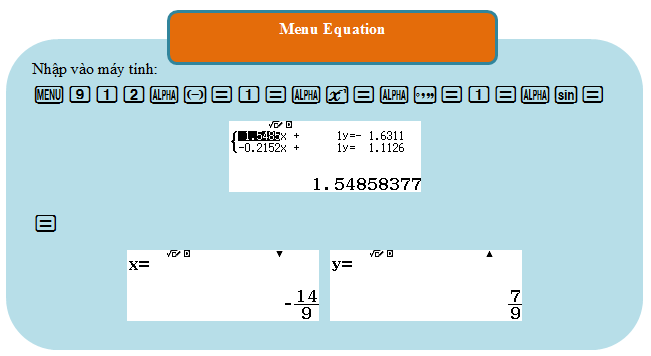
Vậy đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là $y = – \dfrac{{14}}{9}x + \dfrac{7}{9}.$
Cách 2: Tìm được đầy đủ thông tin hai điểm cực trị của đồ thị hàm số thông qua tính năng cực trị của hàm số bậc 3 trên máy tính CASIO fx-580VN X:
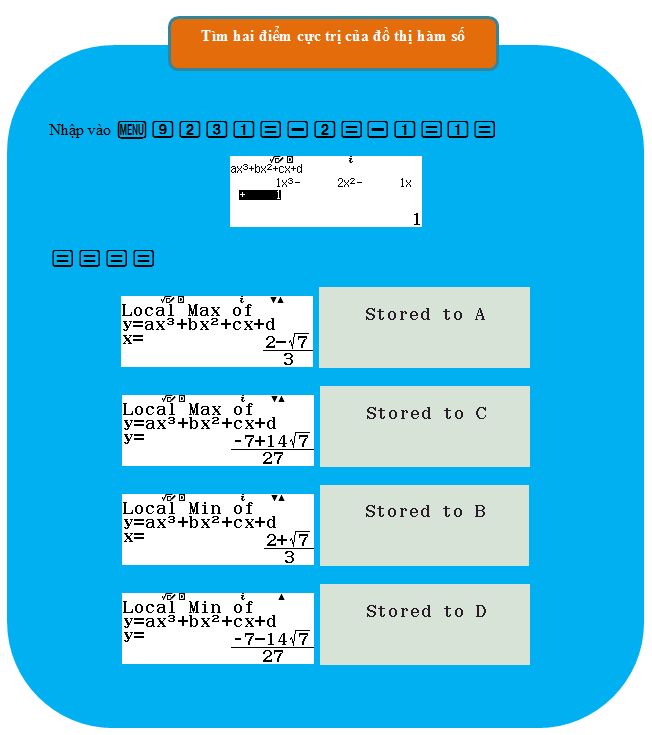
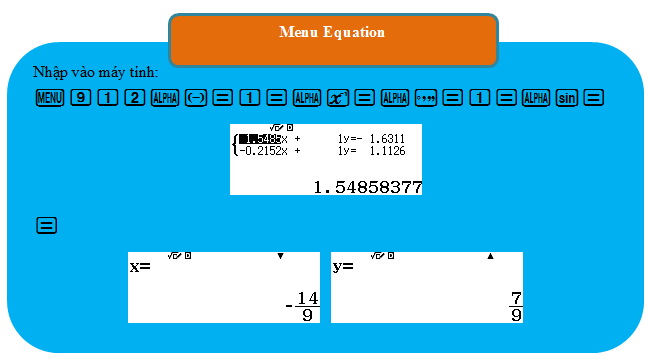
Vậy đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là $y = – \dfrac{{14}}{9}x + \dfrac{7}{9}.$
About TailieuCasio
