Về một số tích phân VDC dẫn đến PTVP
- 07/02/2022
- 233 lượt xem

Bài tích phân này của trường Chuyên Lam Sơn (Thanh Hóa) năm 2022, lời giải được các thầy cô của https://toanmath.com/ trình bày khá chi tiết.
| Ở đây chúng tôi muốn định hướng cho các em học sinh và các thầy cô về lời giải, phòng khi đề bài giữ nguyên dạng thức nhưng có sự thay đổi nhất định về các hàm số. Điều này rất có khả năng xảy ra trong xu thế các trường đại học trọng điểm có khuynh hướng trực tiếp tuyển sinh đại học thông qua kỳ thi đánh giá năng lực chuyên biệt như ĐHSP TP HCM đang tiến hành. |
Ta xét phương trình như sau:
$$y’=y.p(x)+q(x)$$
ở đây để cho gọn ta viết $y$ thay cho $f(x)$ và $y’$ thay cho $f'(x)$.
- $\color{blue}\bullet$ Gọi $P(x)$ là một nguyên hàm của $p(x)$. Đặt $u(x)=e^{-P(x)}$.
- $\color{blue}\bullet$ Nhân hai vế của phương trình đã cho với $u(x)$. Phương trình tương đương với $$y’.u(x)+y.u'(x)=q(x).u(x)$$
- $\color{blue}\bullet$ Vế trái là đạo hàm của $y.u(x)$ nên lấy tích phân xác định hai vế từ $a$ đến $b$ ta có: $$y.u(x)\Big|_a^b=\int_a^bq(x).u(x)dx$$
Áp dụng:
$p(x)=\cot x \Rightarrow P(x)=\ln\sin x$ (ta xét $x \in\left[\dfrac{\pi}{6};\dfrac{\pi}{2}\right]$). Đặt $u(x)=e^{-P(x)}=\dfrac{1}{\sin x}$. Nhân hai vế của phương trình cho $u(x)$. Ta có:
$$\left(f(x).\dfrac{1}{\sin x}\right)’=2x\Rightarrow f(x).\dfrac{1}{\sin x}\Big|_{\frac{\pi}{6}}^{\frac{\pi}{2}}=\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}2xdx$$
Vậy $\dfrac{\pi^2}{4}-2f\left(\dfrac{\pi}{6}\right)=$
Cuối cùng 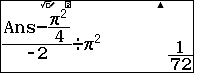
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay