BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
PHẦN 6: GIẢI QUYẾT NHỮNG BÀI TOÁN LUỸ THỪA MA TRẬN BẰNG PHƯƠNG THỨC MATRIX (II)
- 30/01/2019
- 2,248 lượt xem
Trong loạt bài viết này ad đưa ra những hướng dẫn cơ bản nhất để có thể làm quen với phương thức Matrix. Từ đó ứng dụng nó để giải quyết những bài toán Đại số tuyến tính từ đơn giản đến phức tạp. Ngoài ra, loạt bài viết này còn ứng dụng phương thức ma trận để giải quyết một số bài toán trắc nghiệm ở chương trình trung học phổ thông. Phần 6 này ad sẽ sử dụng phương thức matrix để làm cái mà nó làm tốt nhất: giải quyết những bài toán về ma trận.
Trong loạt bài viết này ad đưa ra những hướng dẫn cơ bản nhất để có thể làm quen với phương thức Matrix (ma trận). Từ đó ứng dụng nó để giải quyết những bài toán Đại số tuyến tính từ đơn giản đến phức tạp. Ngoài ra, loạt bài viết này còn ứng dụng phương thức ma trận để giải quyết một số bài toán trắc nghiệm ở chương trình trung học phổ thông. Phần 6 này ad sẽ sử dụng phương thức matrix để làm cái mà nó làm tốt nhất: giải quyết những bài toán về ma trận.
IV Sử dụng phương thức matrix để giải quyết một số bài toán về ma trận
2. Giải quyết những bài toán ma trận bằng phương pháp nhị thức Newton
Bài toán ma trận 6:
Cho ma trận $latex M=\left( \begin{matrix} 2 & 1 \\ 1 & 2 \\\end{matrix} \right)$. Tính $latex {{M}^{n}}$ ứng với mọi $latex n$ nguyên dương cho trước.
(Trích đề thi Olympic Toán sinh viên toàn quốc năm 1995)
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Ta có: $latex M=\left( \begin{matrix} 2 & 1 \\ 1 & 2 \\\end{matrix} \right)=\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)+\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)=A+{{I}_{2}}$
Nhập ma trận $latex A,{{I}_{2}}$ vào máy tính
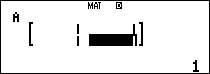
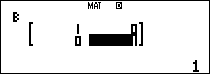
Ta tính thử một số ma trận luỹ thừa của $latex A$:
$latex {{A}^{2}}$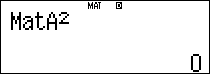
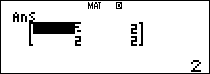
$latex {{A}^{3}}$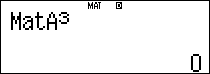
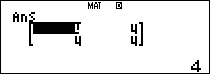
$latex {{A}^{4}}$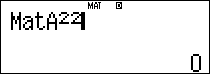
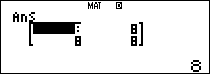
Vậy ta có thể dự đoán $latex {{A}^{n}}=\left( \begin{matrix} {{2}^{n-1}} & {{2}^{n-1}} \\ {{2}^{n-1}} & {{2}^{n-1}} \\\end{matrix} \right)={{2}^{n-1}}\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)$.
Chứng minh quy nạp ta được $latex {{A}^{n}}={{2}^{n-1}}\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)$.
Từ đó ta có:
$$ {{M}^{n}}={{\left( A+{{I}_{2}} \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{A}^{n-k}}{{I}_{2}}^{k}} = \sum\limits_{k=0}^{n-1}{C_{n}^{k}{{2}^{n-k-1}}A}+{{I}_{2}}=\dfrac{{{3}^{n}}-1}{2}A+{{I}_{2}} =\left[ \begin{matrix} \dfrac{{{3}^{n}}+1}{2} & \dfrac{{{3}^{n}}-1}{2} \\ \dfrac{{{3}^{n}}-1}{2} & \dfrac{{{3}^{n}}+1}{2} \\ \end{matrix} \right]$$
Vậy $latex {{M}^{n}}=\left[ \begin{matrix} \dfrac{{{3}^{n}}+1}{2} & \dfrac{{{3}^{n}}-1}{2} \\ \dfrac{{{3}^{n}}-1}{2} & \dfrac{{{3}^{n}}+1}{2} \\\end{matrix} \right]$.
*Trên máy tính Casio fx-580VN X
Ta có: $M=\left( \begin{matrix} 2 & 1 \\ 1 & 2 \\\end{matrix} \right)=\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)+\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)=A+{{I}_{2}}$
Nhập ma trận $A$ vào máy tính
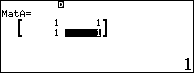
Ta tính thử một số ma trận luỹ thừa của $A$:
${{A}^{2}}$
${{A}^{3}}$
${{A}^{4}}$
Vậy ta có thể dự đoán ${{A}^{n}}=\left( \begin{matrix} {{2}^{n-1}} & {{2}^{n-1}} \\ {{2}^{n-1}} & {{2}^{n-1}} \\\end{matrix} \right)={{2}^{n-1}}\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)$.
Chứng minh quy nạp ta được ${{A}^{n}}={{2}^{n-1}}\left( \begin{matrix} 1 & 1 \\ 1 & 1 \\\end{matrix} \right)$.
Từ đó ta có:
$$ {{M}^{n}}={{\left( A+{{I}_{2}} \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{A}^{n-k}}{{I}_{2}}^{k}}=\sum\limits_{k=0}^{n-1}{C_{n}^{k}{{2}^{n-k-1}}A}+{{I}_{2}}=\dfrac{{{3}^{n}}-1}{2}A+{{I}_{2}}=\left[ \begin{matrix} \dfrac{{{3}^{n}}+1}{2} & \dfrac{{{3}^{n}}-1}{2} \\ \dfrac{{{3}^{n}}-1}{2} & \dfrac{{{3}^{n}}+1}{2} \\\end{matrix} \right]$$
Vậy $latex {{M}^{n}}=\left[ \begin{matrix} \dfrac{{{3}^{n}}+1}{2} & \dfrac{{{3}^{n}}-1}{2} \\ \dfrac{{{3}^{n}}-1}{2} & \dfrac{{{3}^{n}}+1}{2} \\\end{matrix} \right]$.
Lời bình. Khi gặp một số ma trận khó tìm được công thức chung như bài toán trên, chúng ta thử tách ma trận đã cho thành tổng của 2 ma trận có thể dự đoán được công thức chung (thông thường là ma trận luỹ linh và ma trận luỹ đẳng).
Sau đây là một số bài toán tương tự
Bài toán ma trận 7:
Cho ma trận $latex A=\left[ \begin{matrix} 1 & -2 & 1 \\ -1 & 1 & 0 \\ -2 & 0 & 1 \\\end{matrix} \right]$. Hãy tính $latex {{A}^{100}}$.
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Đặt $latex A=B+{{I}_{3}}$
$latex B=\left( \begin{matrix} 0 & -2 & 1 \\ -1 & 0 & 0 \\ -2 & 0 & 0 \\\end{matrix} \right)$, từ đó $latex {{B}^{2}}=\left( \begin{matrix} 0 & 0 & 0 \\ 0 & 2 & -1 \\ 0& 4 & -2 \\\end{matrix} \right)$;$latex {{B}^{3}}=\left[ 0 \right]$
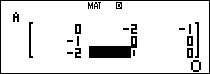
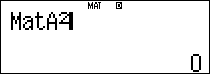
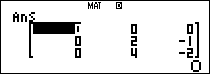
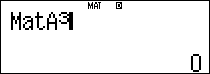
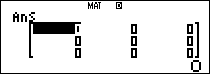
Dùng khai triển New-ton, ta có:
$$ {{A}^{100}}={{\left( B+{{I}_{3}} \right)}^{100}}={{I}_{3}}+100B+\dfrac{100.99}{2}{{B}^{2}}$$
Suy ra $latex {{A}^{100}}=\left( \begin{matrix} 1 & -200 & 100 \\ -100 & 9901 & -4950 \\ -200 & 19800 & -9899 \\\end{matrix} \right)$
*Trên máy tính Casio fx-580VN X
Đặt $latex A=B+{{I}_{3}}$
$latex B=\left( \begin{matrix} 0 & -2 & 1 \\ -1 & 0 & 0 \\ -2 & 0 & 0 \\\end{matrix} \right)$, từ đó $latex {{B}^{2}}=\left( \begin{matrix} 0 & 0 & 0 \\ 0 & 2 & -1 \\ 0 & 4 & -2 \\\end{matrix} \right)$;$latex {{B}^{3}}=\left[ 0 \right]$
Dùng khai triển New-ton, ta có:
$$ {{A}^{100}}={{\left( B+{{I}_{3}} \right)}^{100}}={{I}_{3}}+100B+\dfrac{100.99}{2}{{B}^{2}}$$
Suy ra $latex {{A}^{100}}=\left( \begin{matrix} 1 & -200 & 100 \\ -100 & 9901 & -4950 \\ -200 & 19800 & -9899 \\\end{matrix} \right)$
Bài toán ma trận 8:
Cho ma trận $latex A=\left( \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\\end{matrix} \right)$. Tính ma trận $latex {{A}^{n}}$.
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Ta có: $latex A=\left( \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\\end{matrix} \right)=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\end{matrix} \right)+\left( \begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\\end{matrix} \right)={{I}_{3}}+B$
Mà $latex {{B}^{2}}=\left( \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{matrix} \right);{{B}^{3}}=\left( \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{matrix} \right)$.
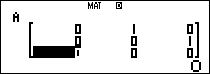
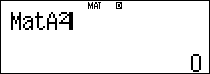
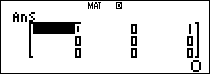
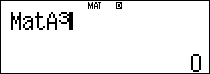
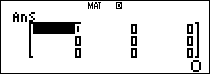
Nên ta có
$$ \Rightarrow {{A}^{n}}={{\left( {{I}_{3}}+B \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{I}^{n-k}}{{B}^{k}}}=I+C_{n}^{1}B+C_{n}^{2}{{B}^{2}} =I+nB+\dfrac{n\left( n-1 \right)}{2}{{B}^{2}}=\left[ \begin{matrix} 1 & n & \dfrac{n\left( n-1 \right)}{2} \\ 0 & 1 & n \\ 0 & 0 & 1 \\\end{matrix} \right]$$
Vậy $latex {{A}^{n}}=\left[ \begin{matrix} 1 & n & \dfrac{n\left( n-1 \right)}{2} \\ 0 & 1 & n \\ 0 & 0 & 1 \\\end{matrix} \right]$
*Trên máy tính Casio fx-580VN X
Ta có: $latex A=\left( \begin{matrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\\end{matrix} \right)=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\end{matrix} \right)+\left( \begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\\end{matrix} \right)={{I}_{3}}+B$
Mà $latex {{B}^{2}}=\left( \begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{matrix} \right);{{B}^{3}}=\left( \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{matrix} \right)$
Nên ta có
$$ \Rightarrow {{A}^{n}}={{\left( {{I}_{3}}+B \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{I}^{n-k}}{{B}^{k}}}=I+C_{n}^{1}B+C_{n}^{2}{{B}^{2}}=I+nB+\dfrac{n\left( n-1 \right)}{2}{{B}^{2}}=\left[ \begin{matrix} 1 & n & \dfrac{n\left( n-1 \right)}{2} \\ 0 & 1 & n \\ 0 & 0 & 1 \\\end{matrix} \right]$$
Vậy $latex {{A}^{n}}=\left[ \begin{matrix} 1 & n & \dfrac{n\left( n-1 \right)}{2} \\ 0 & 1 & n \\ 0 & 0 & 1 \\\end{matrix} \right]$
Bài toán ma trận 9:
Cho ma trận $latex A=\left( \begin{matrix} 2 & -1 & 0 & 0 \\ 0 & 2 & -1 & 0 \\ 0 & 0 & 2 & -1 \\ 0 & 0 & 0 & 2 \\\end{matrix} \right)$. Hãy tính$latex {{A}^{n}}$.
Hướng dẫn
*Trên máy tính Casio fx-580VN X
Ta có:$latex A=\left( \begin{matrix} 2 & -1 & 0 & 0 \\ 0 & 2 & -1 & 0 \\ 0 & 0 & 2 & -1 \\ 0 & 0 & 0 & 2 \\\end{matrix} \right)=2\left( \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right)-\left( \begin{matrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\\end{matrix} \right)=2I-B$
Ta lại có: $latex {{B}^{2}}=\left( \begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\\end{matrix} \right);{{B}^{3}}=\left( \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\\end{matrix} \right)$
Từ đó, ta có thể tính ${{A}^{n}}$ bằng cách khai triển nhị thức Newton như sau
$$\begin{align}
{{A}^{n}}={{\left( 2{{I}_{4}}-B \right)}^{n}}&=\sum\limits_{k=0}^{n}{C_{n}^{k}{{2}^{n-k}}{{I}^{n-k}}{{\left( -1 \right)}^{k}}{{B}^{k}}}={{2}^{n}}I-C_{n}^{1}{{2}^{n-1}}B+C_{n}^{2}{{2}^{n-2}}{{B}^{2}}-C_{n}^{3}{{2}^{n-3}}{{B}^{3}} \\
&={{2}^{n}}I-n{{2}^{n-1}}B+\dfrac{n\left( n-1
\right)}{2}{{2}^{n-2}}{{B}^{2}}-\dfrac{n\left( n-1 \right)\left( n-2
\right)}{6}{{2}^{n-3}}{{B}^{3}}\\
&=\begin{bmatrix}
{{2}^{n}} & -n{{2}^{n-1}} & \dfrac{n\left( n-1 \right)}{2}{{2}^{n-2}} &
-\dfrac{n\left( n-1 \right)\left( n-2 \right)}{6}{{2}^{n-3}} \\
0 & {{2}^{n}} & -n{{2}^{n-1}} & \dfrac{n\left( n-1 \right)}{2}{{2}^{n-2}} \\
0 & 0 & {{2}^{n}} & -n{{2}^{n-1}} \\
0 & 0 & 0 & {{2}^{n}} \\
\end{bmatrix}
\end{align}$$
———————————————-
Trên đây là hướng dẫn giải quyết một số bài toán ma trận bằng máy tính casio fx-570VN Plus và casio fx-580 VNXl. Các bạn xem trên điện thoại thấy có chỗ nào chưa đẹp thì báo lại để mình chỉnh sửa nhá. Cám ơn rất nhiều.
Đón xem phần 7: PHẦN 7: GIẢI QUYẾT NHỮNG BÀI TOÁN LUỸ THỪA MA TRẬN BẰNG PHƯƠNG THỨC MATRIX (III)
Bài viết trước: PHẦN 5: GIẢI QUYẾT NHỮNG BÀI TOÁN LUỸ THỪA MA TRẬN BẰNG PHƯƠNG THỨC MATRIX
About Bitex Khánh Vũ
