KIỂM TRA TÍNH BIẾN THIÊN HÀM SỐ TRÊN CASIO FX 580VNX (Phần 3)
- 05/09/2018
- 1,338 lượt xem
Tính năng TABLE trên máy tính cầm tay CASIO fx 580VNX có thể tích hợp chức năng tính đạo hàm của hàm số tại một điểm, vận dụng linh hoạt chức năng này có thể giúp chúng ta nhanh chóng xác định được tính biến thiên hàm số trên một khoảng.
Bài toán kiểm tra nhanh tính biến thiên hàm số: Điều kiện của tham số $latex m$ để hàm số $latex f(x)=\dfrac{{{x}^{2}}+m({{m}^{2}}-1)x-{{m}^{3}}-1}{x-1}$ đồng biến trên khoảng $latex (-\infty ;1)$
|
Lời giải tự luận:
TXĐ: $latex D=\mathbb{R}\backslash \{1\}$
Ta có: $latex f'(x)=\dfrac{{{x}^{2}}-2x+m+1}{{{(x-1)}^{2}}},\forall x\ne 1$ do đó dấu của $latex f'(x)$ phụ thuộc vào dấu của $latex g(x)={{x}^{2}}-2x+m+1$. Ta có $latex \Delta’ = -m$.
Trường hợp 1: $latex \Delta’ \le 0\Leftrightarrow m\ge 0$, ta có $latex g(x)\ge 0,\forall x\Rightarrow f'(x)\ge 0,\forall x\ne 1$ khi đó hàm số đã cho đồng biến trên $latex (-\infty ,1)$ và $(1,+\infty )$ nên thoả yêu cầu đề bài.
Trường hợp 2: $latex \Delta’ >0\Leftrightarrow m<0$, khi đó phương trình $latex f'(x)=0$ có hai nghiệm $latex {{x}_{1}},{{x}_{2}}({{x}_{1}}<1<{{x}_{2}})$.
Ta có bảng biến thiên của hàm số như sau:
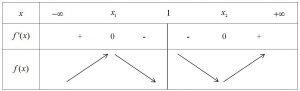
Từ bảng biến thiên, ta thấy trong trường hợp này không có giá trị nào của $latex m$ thoả mãn yêu cầu bài toán.
Kết luận với $latex m\ge 0$ thì hàm số $latex f(x)$ đồng biến trên $latex (-\infty ;1)$.
Vậy ta chọn đáp án C.
Một chức năng hữu ích của CASIO fx 580VNX là trong phương thức TABLE chúng ta có thể nhập biểu thức tính đạo hàm (Dòng máy tính fx570VN Plus không thể nhập biểu thức đạo hàm). Ta có thể dùng tính năng này để kiểm tra kết quả bài toán trên bằng chức năng TABLE, cụ thể ở đây ta sẽ kiểm tra với $latex m=3$ như sau
Bước 1: Mở phương thức TABLE
- Cách bấm: w8
- Máy tính hiển thị:

Bước 2: Nhập biểu thức $latex \dfrac{d}{dx}{{\left. \left( \frac{{{x}^{2}}+3({{3}^{2}}-1)x-{{3}^{3}}-1}{x-1} \right) \right|}_{x=x}}$
- Cách bấm: qya[d+3(3dp1 [p3qdp1R[p1$$[
- Máy tính hiển thị:

Bước 3: Nhập thông số START, END, STEP. Vì ta đang cần kiểm tra tính nghịch biến trên khoảng $latex (0;2)$ nên ta chọn $latex START=-10,END=1,STEP=\dfrac{1–(-10)}{29}=\dfrac{11}{29}$
- Cách bấm: ==p10=1=11P29=
- Máy tính hiển thị:
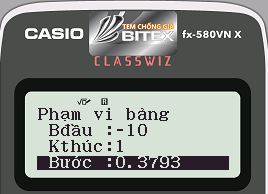
Bước 4: Nhấn phím = và nhận xét kết quả
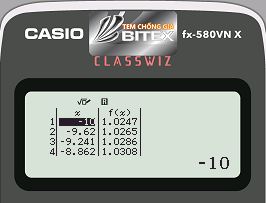
Ta thấy $latex f'(x)>0,\forall x\in (-10;1)$ do đó $latex m=3$ thoả yêu cầu bài toán từ đó ta loại đáp án A, B và D.
Xem lại Kiểm tra nhanh tính biến thiên hàm số trên casio fx 580vnx (phần 2)
Xem lại Kiểm tra nhanh tính biến thiên hàm số trên casio fx 580vnx (phần 1)
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay