Khối đa diện tạo bởi một tứ giác và một đoạn thẳng vẽ ngoài mặt phẳng chứa tứ giác đó

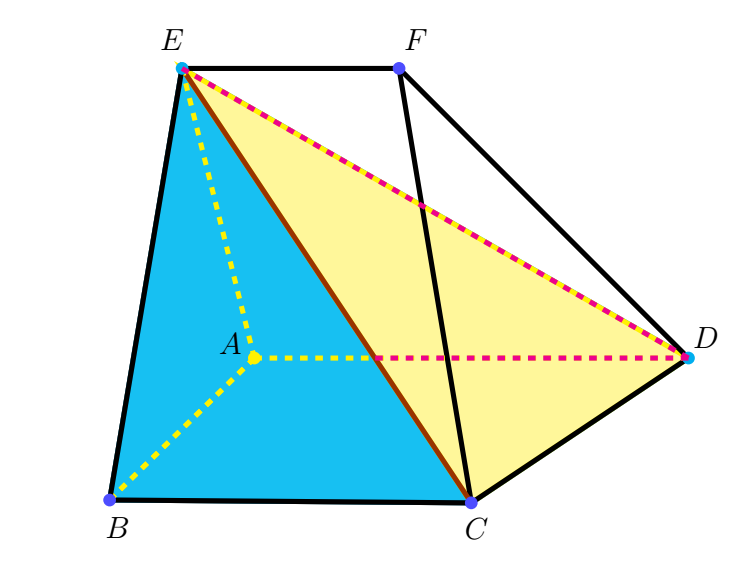
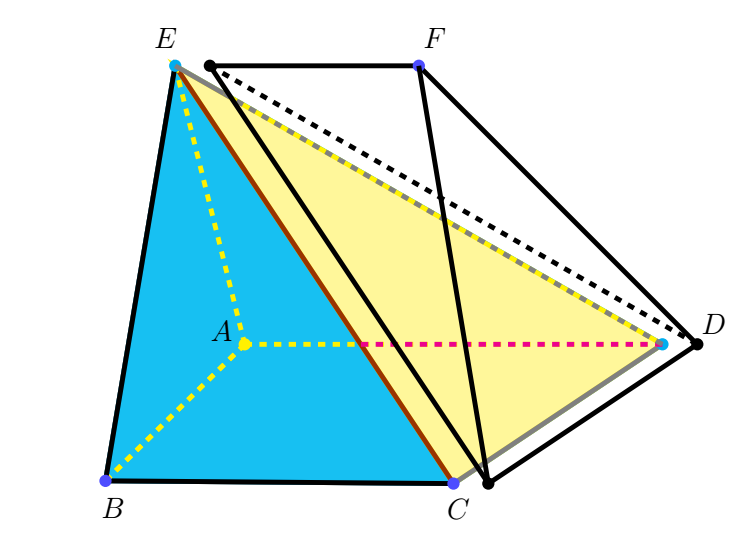
Đề thi thử Chuyên Vinh lần 2 / 2020

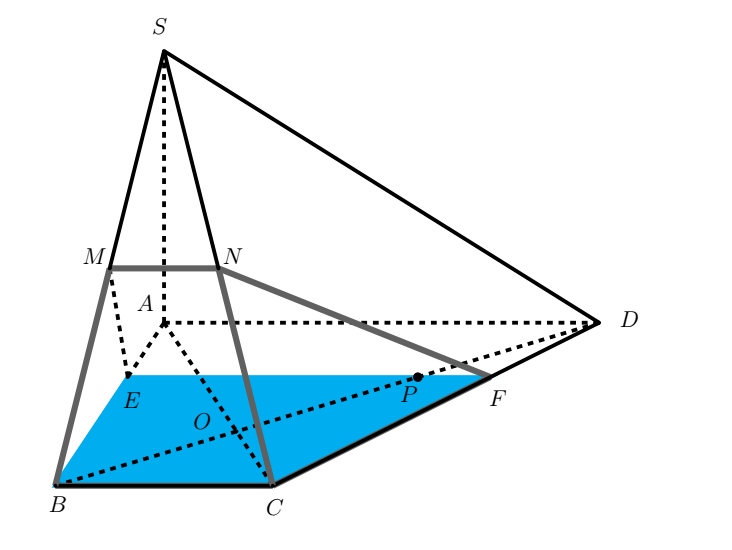
Chọn hệ trục $Axyz$ sao cho tia $Ax$ đi qua $B$, tia $Ay$ đi qua $D$ và tia $Az$ đi qua $S$, chọn $a$ làm 1 đơn vị chiều dài.

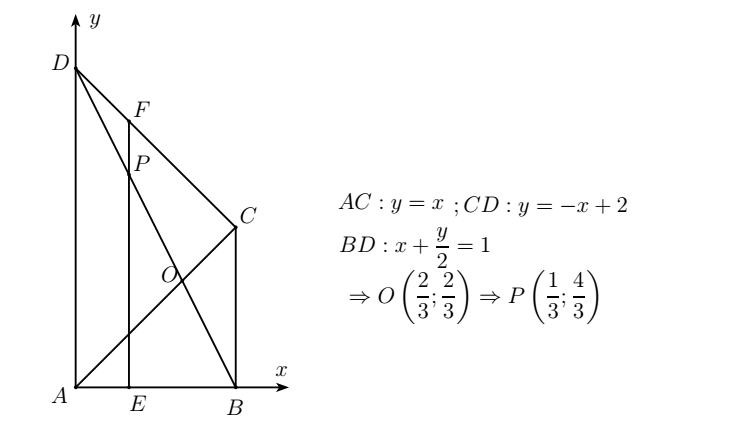
Tung độ điểm $F$ là $\dfrac53$ do đó $EF=\dfrac53 BC \Rightarrow S_{ECF}=\dfrac53S_{ECB}$.

Thể tích của khối đa diện cần tìm bằng $$V=V_{MBEC}+V_{MECF}+V_{MNCF}$$ trong đó $V_{MECF}=\dfrac53V_{MBEC}$

Vậy

Ta có tọa độ các điểm 

$$B(1;0;0), C(1;1;0),E\left(\dfrac13;0;0\right),F\left(\dfrac13;\dfrac53;0\right)$$ $$M\left(\dfrac12;0;1\right),N\left(\dfrac12;\dfrac12;1\right)$$ 

Để tìm thể tích của tứ diện ta lấy $\dfrac16$ giá trị tuyệt đối của định thức của ma trận cấp 4 mà mỗi dòng của ma trận là tọa độ của các đỉnh, riêng thành phần thứ 4 ta gán cho 1. 

e

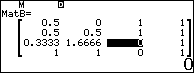
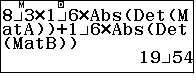
nhân cho đv thể tích $a^3$, ta chọn B.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.