BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải câu 38 mã đề 101 trên Casio
- 11/08/2020
- 151 lượt xem
| Câu 38. Cho $a$ và $b$ là hai số thực dương thỏa mãn $4^{ \log_2(a^2b)} = 3a^3$. Giá trị của $ab^2$ bằng A. $3.\qquad \qquad \qquad \quad $ B. $6.\qquad \qquad \qquad \quad$ C. $12.\qquad \qquad \qquad \quad$ D. $2.\qquad \qquad \qquad \quad$ |
Giải
- Lấy một số ngẫu nhiên lưu vào A.
- Viết lên màn hình
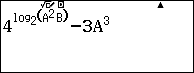
- Ra lệnh giải phương trình Shift Solve , máy hỏi A ta chấp nhận bằng cách bấm mũi tên xuống, máy hỏi B ta nhập 0 và cuối cùng sẽ được nghiệm tự động lưu vào B.
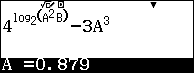
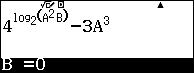
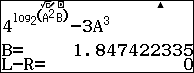
- Tính
ta chọn A.
Chia sẻ
About TS. Nguyễn Thái Sơn
