BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải câu 37 ĐMH 2018 bằng tư duy kết hợp với máy tính
- 01/02/2018
- 252 lượt xem
Câu 37. Cho hàm số [latex]f(x)[/latex] xác định trên [latex]\mathbb R\backslash\{\dfrac12\}[/latex] thỏa mãn [latex]f'(x)=\dfrac2{2x-1}[/latex], [latex]f(0)=1[/latex] và [latex]f(1)=2[/latex]. Giá trị của biểu thức [latex]f(-1)+f(3)[/latex] bằng
A. [latex]4+\ln15[/latex].
B. [latex]2+\ln15[/latex]
C. [latex]3+\ln15[/latex].
D. [latex]\ln15[/latex].
Lời giải
Ta có : [latex]f\left( x \right)=\int{{f}’\left( x \right)\text{d}x}=2\int{\dfrac{1}{2x-1}\text{d}x}=\dfrac{2}{2}\ln \left| 2x-1 \right|+C=\ln \left| 2x-1 \right|+C.[/latex]
Ta có: [latex]f\left( -1 \right)-f\left( 0 \right)=\int\limits_{0}^{-1}{{f}’\left( x \right)\text{d}x}=\int\limits_{0}^{-1}{\dfrac{2}{2x-1}\text{d}x}=\left. \ln \left| 2x-1 \right| \right|_{0}^{-1}=\ln 3.[/latex] [latex]f\left( 3 \right)-f\left( 1 \right)=\int\limits_{1}^{3}{{f}’\left( x \right)\text{d}x}=\int\limits_{1}^{3}{\dfrac{2}{2x-1}\text{d}x}=\left. \ln \left| 2x-1 \right| \right|_{1}^{3}=\ln 5.[/latex]
Vậy [latex]f\left( -1 \right)-f\left( 0 \right)+f\left( 3 \right)-f\left( 1 \right)=\ln 3+\ln 5\Leftrightarrow f\left( -1 \right)+f\left( 3 \right)=\ln 3+\ln 5+3\Leftrightarrow f\left( -1 \right)+f\left( 3 \right)=\ln 15+3[/latex]
Giải trên máy tính CASIO fx-570VN PLUS:
Nhập vào máy tính: [latex]\int\limits_{0}^{-1}{\dfrac{2}{2x-1}\text{d}x}+\int\limits_{1}^{3}{\dfrac{2}{2x-1}\text{d}x}+1+2[/latex], thu được:
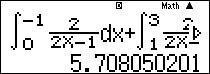
So sánh đáp án, chọn C.
Mẹo: Để ý phép toán cần thực hiện là [latex]f\left( -1 \right)+f\left( 3 \right)[/latex] nên [latex]x=-1;x=3[/latex] đều phải đóng vai trò là cận trên hoặc cận dưới của tích phân.
About TailieuCasio
