BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI BẤT PHƯƠNG TRÌNH MŨ- LOGARIT VỚI CASIO FX 580VNX
- 01/10/2019
- 2,077 lượt xem
Bất phương trình mũ và logarit là 1 chuyên đề mà học sinh rất Ứng dụng máy tính cầm tay là một phương pháp làm hiệu quả để chọn được đáp án nhanh và chính xác dành cho các bài toán trắc nghiệm liên quan đến bất phương trình mũ-logarit. Và Diễn đàn Toán Casio đã tìm hiểu và trình bày một số ví dụ sử dụng lệnh TABLE để tìm kết quả cho bài toán bất phương trình mũ logarit
Bài toán 1. Tìm tập nghiệm của bất phương trình $\dfrac{x+{{3}^{x}}-4}{{{x}^{2}}-x-6}>0$
A. $\left[ \begin{align} & x<-2 \\ & x>3 \\ \end{align} \right.$
B. $\left[ \begin{align} & -1<x<2 \\ & x>3 \\ \end{align} \right.$
C. $\left[ \begin{align} & -2<x<1 \\ & x>3 \\ \end{align} \right.$
D. $x\le 1$
Hướng dẫn giải
Phương pháp sử dụng máy tính Casio
Đặt $f\left( x \right)=x+{{3}^{x}}-4$ và $g\left( x \right)={{x}^{2}}-x-6$
Sử dụng phương thức TABLE w8 để kiểm tra các đáp án. Nếu $f\left( x \right)g\left( x \right)>0$ thì đáp án đó đúng
Dựa vào các đáp án, ta khảo sát các hàm số trong khoảng $\left[ -4;4 \right]$
Nhập vào hàm số $f\left( x \right)$ và $g\left( x \right)$
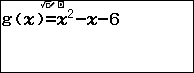
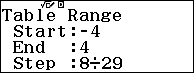
Bảng kết quả thu được là
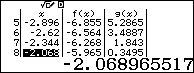
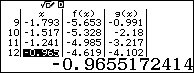
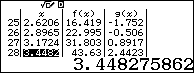
Dựa vào bảng kết quả ta thấy
$f\left( x \right)g\left( x \right)>0\Leftrightarrow \left[ \begin{align} & -2<x<1 \\ & x>3 \\ \end{align} \right.$
Vậy tập nghiệm của phương trình là $\left[ \begin{align}& -2<x<1 \\ & x>3 \\\end{align} \right.$
Đáp án C
Phương pháp tự luận
ĐK: ${{x}^{2}}-x-6\ne 0\Leftrightarrow \left\{ \begin{align} & x\ne -2 \\ & x\ne 3 \\ \end{align} \right.$
Ta có:
$\dfrac{x+{{3}^{x}}-4}{{{x}^{2}}-x-6}>0$
Trường hợp 1. $\left\{ \begin{align} & {{3}^{x}}+x-4>0 \\ & {{x}^{2}}-x-6>0 \\\end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x>1 \\ & x<-2\vee x>3 \\\end{align} \right.$$\Leftrightarrow x>3$
Trường hợp 2. $\left\{ \begin{align} & {{3}^{x}}+x-4<0 \\ & {{x}^{2}}-x-6<0 \\\end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x<1 \\ & -2<x<3 \\\end{align} \right.$$\Leftrightarrow -2<x<1$
Đáp án C
Bài toán 2. Bất phương trình sau đây ${{3}^{{{x}^{2}}-1}}\ge {{2}^{x-1}}$ có tập nghiệm là.
A. ${{\log }_{2}}3-1\le x\le 1$
B. $1\le x\le {{\log }_{2}}3+1$
C. $\left[ \begin{align} & x\ge 1 \\ & x\le {{\log }_{2}}3-1 \\ \end{align} \right.$
D. $\left[ \begin{align} & x\ge 1 \\ & x\le {{\log }_{3}}2-1 \\ \end{align} \right.$
Hướng dẫn giải
Phương pháp sử dụng máy tính Casio
Kiểm tra giá trị ${{\log }_{2}}3,{{\log }_{3}}2$
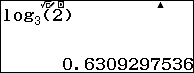
Sử dụng phương thức TABLE w8 để kiểm tra các đáp án.
Điều chỉnh máy tính về chế độ tính toán bảng tính TABLE với một hàm số qwRR11
Nhập vào hàm số $f\left( x \right)={{3}^{{{x}^{2}}-1}}-{{2}^{x-1}}$
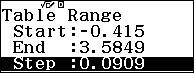
Và bảng giá trị $Start={{\log }_{2}}3-2,End={{\log }_{2}}3+2,Step=\frac{4}{44}$
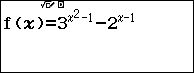
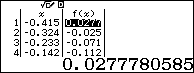
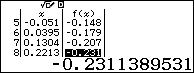
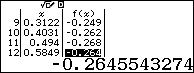
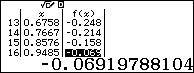
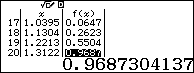
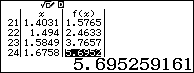
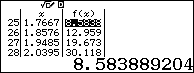
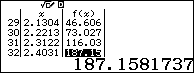
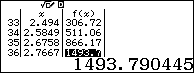
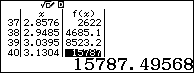
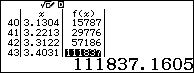
Dựa theo bảng kết quả ta thấy với $x\ge 1$ thì $f\left( x \right)\ge 0$. Suy ra loại A
Ngoài ra dựa vào bảng kết quả ta nhận thấy
- Với $x=3.4031>{{\log }_{2}}3+1$ thì $f\left( x \right)\ge 0$. Suy ra loại B
- Với $x=0.494<{{\log }_{2}}3-1$ thì $f\left( x \right)<0$. Suy ra loại C
Vậy đáp án đúng là D
Phương pháp tự luận
Lấy logarit cơ số 2 hai vế ta được
${{\log }_{2}}{{3}^{({{x}^{2}}-1)}}\ge {{\log }_{2}}{{2}^{(x-1)}}$
$\Leftrightarrow ({{x}^{2}}-1){{\log }_{2}}3\ge (x-1)$
$\Leftrightarrow (x-1)(x+1){{\log }_{2}}3\ge (x-1)$
Trường hợp 1.$\left\{ \begin{align} & x\ge 1 \\ & (x+1)lo{{g}_{2}}3\ge 1 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x\ge 1 \\ & x\ge \frac{1}{{{\log }_{2}}3}-1 \\ \end{align} \right.$$\Leftrightarrow x\ge 1$
Trường hợp 2.$\left\{ \begin{align} & x\le 1 \\ & (x+1)lo{{g}_{2}}3\le 1 \\ \end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x\le 1 \\ & x\le \frac{1}{{{\log }_{2}}3}-1 \\ \end{align} \right.$ $\Leftrightarrow x\le {{\log }_{3}}2-1$
Chọn đáp án D
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
