BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI BẤT PHƯƠNG MŨ TRONG ĐỀ THI TỐT NGHIỆP THPT NĂM 2022 MÔN TOÁN
- 26/07/2022
- 206 lượt xem
ĐỀ BÀI: Có bao nhiêu số nguyên dương $a$ sao cho ứng với mỗi $a$ có đúng hai số nguyên $b$ thỏa mãn $(3^b-3)(a.2^b-16)<0?$
HƯỚNG DẪN GIẢI
$(3^b-3)(a.2^b-16)<0$
$\Leftrightarrow{(3^b-3^1)[2^b-2^{\log_{2}( \dfrac{16}{a} )}]}<0$
$\Leftrightarrow{(b-1)[b-{\log_{2}( \dfrac{16}{a} )}]}<0$
$\Leftrightarrow{\left[\begin{matrix}{1<b<\log_{2}( \dfrac{16}{a} ),\hspace{1cm}nếu\hspace{2mm}1<\log_{2}( \dfrac{16}{a} )\\\log_{2}( \dfrac{16}{a} )<b<1,\hspace{1cm}nếu\hspace{2mm}1>\log_{2}( \dfrac{16}{a} )}\end{matrix}\right.}$
ycbt$\hspace{5mm}\Leftrightarrow{\left[\begin{matrix}{3<\log_{2}( \dfrac{16}{a} ) \leq {4},\\-2 \leq {}\log_{2}( \dfrac{16}{a} )<-1}\end{matrix}\right.}$
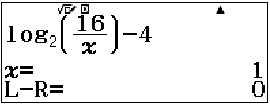
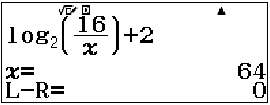
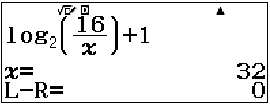
$\Rightarrow{\left[\begin{matrix}{1\leq{a}<2\\32<a \leq{}64}\end{matrix}\right.}$
Vậy $a=1,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64$
Có $33$ số nguyên dương $a$ thỏa yêu cầu bài toán.
Video hướng dẫn giải chi tiết TẠI ĐÂY
About Toanbitexdtgd1
