XÁC ĐỊNH NHANH TÍNH CHẴN LẺ HÀM SỐ LƯỢNG GIÁC TRÊN CASIO FX 580VNX

Sự ra đời dòng máy tính cầm tay CASIO fx 580VNX đã giúp việc giải toán được nhanh và chính xác hơn. Hãy cùng Diễn Đàn Máy Tính Cầm Tay xác định nhanh tính chẵn lẻ hàm số lượng giác dưới đây nhé.

Bài viết mới: SỬ DỤNG MÁY TÍNH CASIO FX 580VNX ĐỂ KIỂM TRA TÍNH CHẴN LẺ CỦA HÀM SỐ LƯỢNG GIÁC- PHẦN 2

Lời giải:

Trước hết ta nhắc lại phương pháp, để xác định tính chẵn lẻ của hàm số ta thực hiện theo các bước sau:

Bước 1: Tìm tập xác định $latex D$ của hàm số, khi đó:

Nếu $latex D$ là một tập đối xứng (tức là $latex \forall x\in D\Rightarrow -x\in D$) thì ta thực hiện tiếp bước 2.

Nếu $latex D$ không là tập đối xứng (tức là $latex \exists x\in D$ mà $-x\notin D$) ta kết luận hàm số không chẵn cũng không lẻ.

Bước 2: Xác định $latex f(-x)$, khi đó:

Nếu $latex f(-x)=f(x)$ ta kết luận hàm số là hàm chẵn

Nếu $latex f(-x)=-f(x)$ ta kết luận hàm số là hàm lẻ.

Ngoài ra ta kết luận hàm số không chẵn cũng không lẻ.

Áp dụng phương pháp trên vào bài toán.

Điều kiện xác định của hàm số là:

$latex \left\{ \begin{align}  & \cos x\ne 0 \\  & \sin x+\tan x\ne 0 \\ \end{align} \right.$

$latex \Leftrightarrow \left\{ \begin{align}  & \cos x\ne 0 \\  & \sin x\left( 1+\frac{1}{\cos x} \right)\ne 0 \\ \end{align} \right.$

$latex \Leftrightarrow \left\{ \begin{align}  & \cos x\ne 0 \\  & \sin x\ne 0 \\ \end{align} \right.$

$latex \Leftrightarrow \sin 2x\ne 0\Leftrightarrow x\ne \frac{k\pi }{2},k\in \mathbb{Z}$

Vậy tập xác định của hàm số là: $latex D=\mathbb{R}\backslash \{x=\dfrac{k\pi }{2},k\in \mathbb{Z}\}$ ($latex D$ là tập đối xứng)

ta có:

$latex f(-x)=\dfrac{{{(-x)}^{3}}}{\sin (-x)+\tan (-x)}=\dfrac{-{{x}^{3}}}{-\sin x-\tan x}=\dfrac{{{x}^{3}}}{\sin x+\tan x}=f(x)$ nên hàm số đã cho là hàm chẵn.

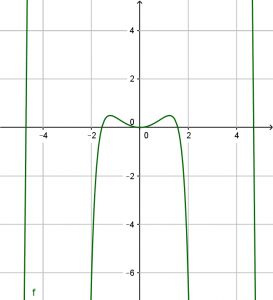
Ta có thể kiểm tra mối quan hệ giữa $latex f(x)$ và $latex f(-x)$  trên máy tính cầm tay CASIO fx 580VNX từ đó ta có thể đưa ra dự đoán về tính chẵn lẻ hàm số, diendanmaytinhcamtay.vn lấy câu a của bài toán để làm ví dụ.

Bước 1: Mở chức năng TABLE

• Cách bấm: w8
• Máy tính hiển thị:

Bước 2: Nhập biểu thức hàm số $latex f(x)=\dfrac{{{x}^{3}}}{\sin x+\tan x}$

• Cách bấm: a[^3Rj[)+l[)
• Máy tính hiển thị:

• Cách bấm: ==pqKP2=qKP2=qKP29=
• Máy tính hiển thị:

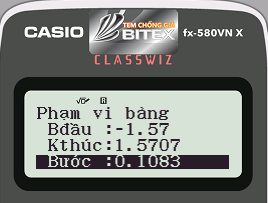
Bước 4: Nhấn phím = và đánh giá bảng kết quả:

Quan sát bảng kết quả ta thấy rằng tại dòng 15 và 16 giá trị của $latex f(x)$ giống nhau, tương tự tại dòng 14 và 17 cũng như vậy (Lưu ý rằng giá trị của $latex x$ tại dòng 15 và 16, 14 và 17 là những cặp giá trị trái dấu) do đó ta dự đoán được $latex f(x)$ là hàm số chẵn.

Vận dụng máy tính cầm tay Casio fx 580VNX một cách hiệu quả có thể giúp chúng ta xác định được tính chẵn lẻ hàm số lượng giác một cách nhanh chóng. Hãy truy cập diendanmaytinhcamtay.vn để nhận được các bài viết hay mỗi ngày.

Bài viết mới: Xác định nhanh tính chẵn lẻ hàm số trên casio fx 580vnx.

About Bitex Casio