BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Vận dụng công thức tìm bán kính mặt cầu ngoại tiếp khối tứ diện
- 07/01/2022
- 463 lượt xem
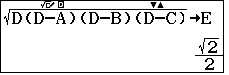
| Ta có công thức: $\color{blue}R=\dfrac{S}{6V}$, trong đó $V$ là thể tích khối tứ diện, $S=\sqrt{p(p-a)(p-b)(p-c)}$ với $a, b, c$ là lần lượt là tích của các cặp cạnh đối diện của khối tứ diện và $p=\dfrac{a+b+c}{2}$. |
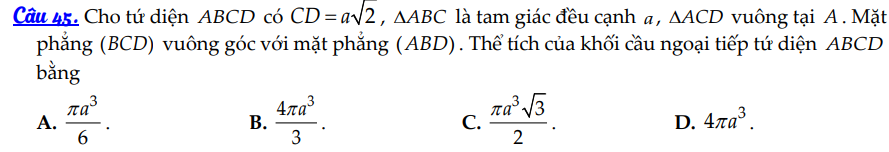
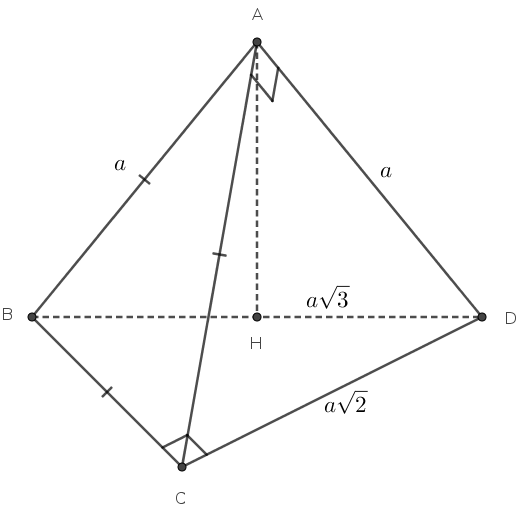
Các cặp cạnh đối diện của khối tứ diện là $AB=a, CD=a\sqrt2\ ; \ AD=a, BC=a\ ; \ BD=a\sqrt3, AC=a$.
|
Phương pháp truyền thống: Trong tam giác $AHD$ vẽ đường trung trực cạnh $AD$ cắt cạnh $AH$ tại $I$. Theo hệ thức lượng trong đường tròn ta có: $$AI.AH=\dfrac{AD^2}{2}\Rightarrow R=\dfrac{AD^2}{2AH}=\dfrac{a^2}{2\sqrt{a^2-\left(\dfrac{a\sqrt3}{2}\right)^2}}=a$$ |
|
Phương pháp dùng công thức: Thể tích khối tứ diện $V=\dfrac13.S_{BCD}.AH=\dfrac13.\dfrac12.a^2\sqrt2.\sqrt{a^2-\left(\dfrac{a\sqrt3}{2}\right)^2}$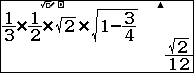 
Tích của các cặp cạnh của khối tứ diện lần lượt là $1; \sqrt2 ; \sqrt3$ (đơn vị) lưu vào A, B, C tương ứng. Trên MTCT không có chữ $p$ ta thay bằng D. |
Vậy thể tích khối cầu $V_{\text{kc}}=\dfrac43\pi R^3=\dfrac{3\pi a^3}{4}$
Nhận xét: Phương pháp truyền thống có lợi thế khi ba cạnh bên cùng một đỉnh bằng nhau. Phương pháp dùng công thức có lợi thế khi gặp một khối tứ diện cho trước 6 cạnh. (Bài toán vận dụng cao).
Chia sẻ
About TS. Nguyễn Thái Sơn
