Từ một bài toán GTNN cổ điển

1. Bài toán mở đầu

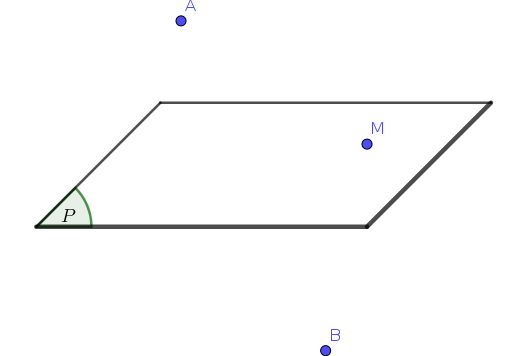
GIẢI

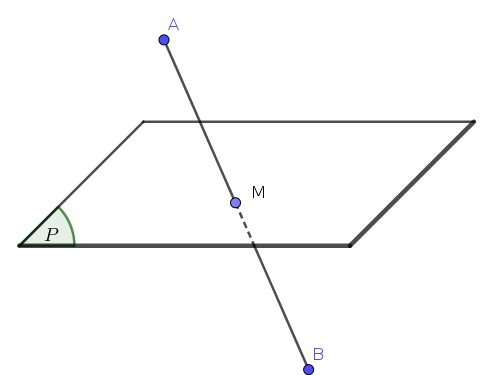
Ta có $AM+BM \geqslant AB =$const

Vì $AB$ là hằng số nên $AM+BM$ đạt giá trị nhỏ nhắt khi và chỉ khi xảy ra dấu “bằng”.

Khi đó $M$ nằm trên đoạn thẳng $AB$.

Vì $A$ và $B$ nằm ở hai phía mặt phẳng $M$ cũng là giao điểm của đường thẳng $AB$ với mặt phẳng $(P)$.

2. Bài toán mở rộng

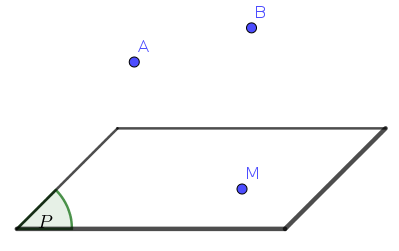
GIẢI

Gợi ý: Nếu ta giải như trên

Do đó ta phải cải tiến thuật toán như sau:

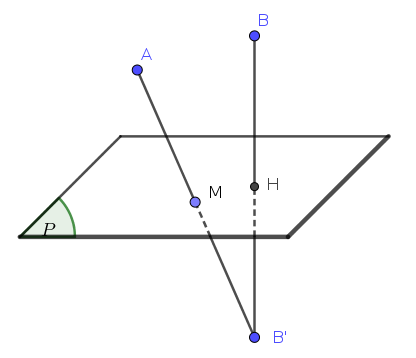
1. 1. Gọi $B’$ là điểm đối xứng của điểm $B$ qua mặt phẳng $(P)$.
2. 2. Khi đó
    

   $AM+BM=AM+B’M \geqslant AB’= \text{cont.}$
    
   Vậy $AM+BM$ nhỏ nhất khi và chỉ khi xảy ra dấu “bằng”. Khi đó $M$ nằm trên đoạn thẳng $AB’$

3. 3. Vì $A$ và $B’$ nằm ở hai phía mặt phẳng $(P)$ nên điểm $M$ như thế tồn tại và là giao điểm của đường thẳng $AB’$  với mặt phẳng $(P)$.

3. Áp dụng bằng số

GIẢI

Lấy toạ độ hai điểm $A$ và $B$ thay vào vế trái của phương trình mặt phẳng , các kết quả cùng dấu (cụ thể là cùng dương) nên $A$ và $B$ nằm ở cùng một phía đối với mặt phẳng $(P)$.
Ta gọi $B’$ là đối đối xứng của $B$ qua mặt phẳng $(P)$.
Toạ độ hình chiếu vuông góc của $B$ trên $(P)$ là nghiệm của hệ phương trình

Nghiệm

Vậy $B'(-17;4;-1)$.
Ta có $AM+BM=AM+B’M \geqslant AB’=$ cont.Vậy $AM+BM$ nhỏ nhất khi và chỉ khi xảy ra dấu “bằng”. Khi đó $M$ nằm trên đoạn thẳng $AB’$
Vì $A$ và $B’$ nằm ở hai phía mặt phẳng $(P)$ nên $M$ cũng là giao điểm của đường thẳng $AB’$ với mặt phẳng $(P)$.
$\overrightarrow{AB’}=(-20;8;-8) // \overrightarrow{u}=(5;-2;2)$.

Toạ độ giao điểm của $AB’$ với mặt phẳng $(P)$ là nghiệm của hệ phương trình

Đáp số $M(-2;-2;5)$.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.