BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng máy tính tìm tọa độ đỉnh, hỗ trợ giải bài toán đồ thị khó
- 19/06/2018
- 871 lượt xem
Xem bài viết mới: XÁC ĐỊNH NHANH TOẠ ĐỘ ĐỈNH, PHƯƠNG TRÌNH TRỤC ĐỐI XỨNG PARABOL TRÊN CASIO FX 580VNX
Bài toán: Cho hàm số [latex]y=f(x)[/latex] có đồ thị [latex]y=f’(x)[/latex] như hình vẽ sau:
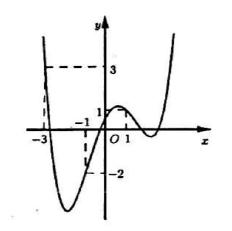
Xét hàm số [latex]g(x)=f(x)-\dfrac{1}{3}x^3-\dfrac{3}{4}x^2+\dfrac{3}{2}x+2018[/latex], mệnh đề nào sau đây đúng?
- [latex]\text{min}_{[-3;\,1]}g(x)=g(-3)[/latex].
- [latex]\text{min}_{[-3;\,1]}g(x)=g(-1)[/latex].
- [latex]\text{min}_{[-3;\,1]}g(x)=g(1)[/latex].
- [latex]\text{min}_{[-3;\,1]}g(x)=\dfrac{g(-3)+g(1)}{2}[/latex].
Bài giải
Để xét min, max của hàm số, cần tính đạo hàm: [latex]g’(x)=f’(x)-x^2-\dfrac{3}{2}x+\dfrac{3}{2}[/latex].
[latex]g’(x)=0 \Leftrightarrow f’(x)=x^2+\dfrac{3}{2}x-\dfrac{3}{2}[/latex].Nhận xét đồ thị hàm số [latex]f’(x)[/latex] giao với đồ thị hàm số [latex] y=x^2+\dfrac{3}{2}x-\dfrac{3}{2}[/latex] tại các điểm đặc biệt như [latex](-3;\,3),\,(-1;\,-2),\,(1;\,1)[/latex].
Sử dụng máy tính CASIO fx-570VN PLUS để tìm nhanh tọa độ đỉnh của Parabol [latex]y=x^2+\dfrac{3}{2}x-\dfrac{3}{2}[/latex]:
Nên thu được trên khoảng [latex][-3;\,-1][/latex] thì [latex]f’(x)\leq x^2+\dfrac{3}{2}x-\dfrac{3}{2}[/latex] và trên khoảng [latex][-1;\,1][/latex] thì [latex]f’(x)\geq x^2+\dfrac{3}{2}x-\dfrac{3}{2}[/latex].
Lập bảng biến thiên thu được giá trị nhỏ nhất của [latex]g(x)[/latex] trên đoạn [latex][-3;\,1][/latex] là [latex]g(-1)[/latex].
About TailieuCasio
