Giải nhanh hệ bốn phương trình tuyến tính trên Casio fx 580VN X
- 14/12/2021
- 2,105 lượt xem
So với dòng máy tính Casio Fx570VN Plus việc đưa chức năng giải hệ bốn phương trình tuyến tính là sự nâng cấp cần thiết và cực kỳ hữu ích. Trong tài liệu này chúng tôi chỉ giới thiệu tính năng, việc vận dụng tính năng này trong thực tế giải toán sẽ được trình bày chi tiết trong các tài liệu nâng cao.
Ví dụ Trong không gian với hệ trục toạ độ $\large Oxyz$, cho hai đường thẳng
$\large d_1: \left\{\begin{matrix} x=1+3t & \\ y=-2+t & \\ z=2 & \end{matrix}\right.$ $\large ;d_2:\dfrac{x-1}{2}=\dfrac{y+2}{-1}=\dfrac{z}{2}$ và mặt phẳng $\large (P): 2x+2y-3z=0$. Phương trình mặt phẳng đi qua giao điểm của $\ d_1 $ và $\(P) $ đồng thời vuông góc với $\ d_2 $ là:
A. $\large 2x−y+2z+22=0$
B. $\large2x−y+2z−13 = 0$
C. $\large2x−y+2z+13 = 0$
D. $\large2x+y+2z−22 = 0$
Do vectơ pháp tuyến là $\large \bar{n}=(2;−1;2)$ nên loại D, ba phương án còn lại chỉ khác nhau ở hệ số tự do, tạo thành khi thay toạ độ giao điểm vào phần còn lại của biểu thức. Ta xác định toạ độ giao điểm trên máy tính như sau:
w914 nhập hệ số của hệ phương trình:
$\large \left\{\begin{matrix} x=1+3t & \\ y=-2+t & \\ z=2 & \\ 2x+2y-3z=0 & \end{matrix}\right.$
Hệ số của $\large t $ đúng ra là phải được chuyển sang vế trái, tuy nhiên $\large t $ không đóng vai trò gì trong toạ độ giao điểm nên để thuận tiện ta giữ hệ số của $\large t $ ở vế phải nhập vào máy tính.
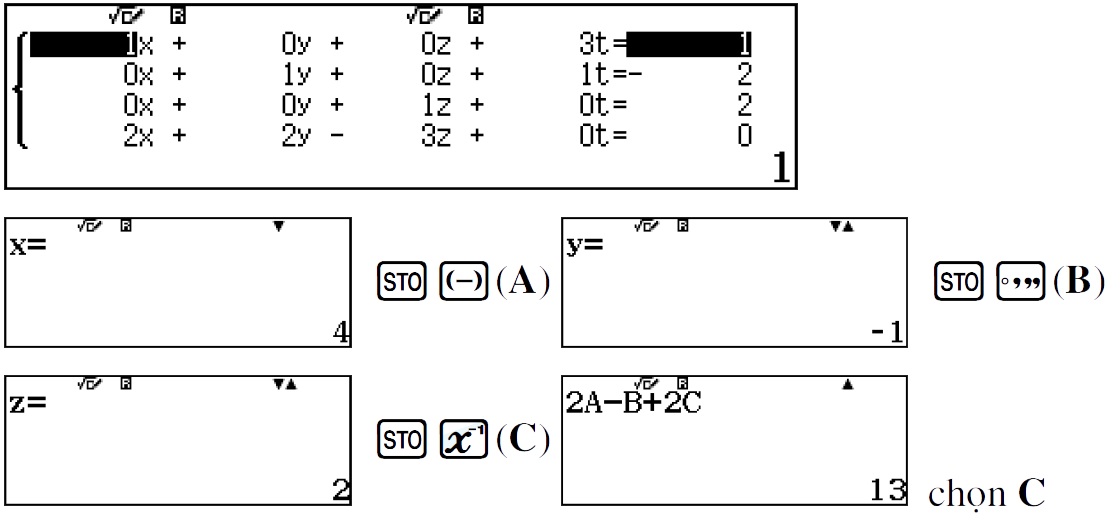
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay