BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
XÁC ĐỊNH NHANH CÁC HỆ SỐ HÀM SỐ BẬC 2 TRÊN CASIO FX 580VNX
- 05/09/2018
- 1,334 lượt xem
Bài toán tìm các hệ số hàm số bậc 2 với các điều kiện cho trước là một bài toán quen thuộc trong chương II, chương trình Đại số lớp 10. Diendanmaytinhcamtay.vn xin hướng dẫn các bạn cách sử dụng máy tính cầm tay CASIO fx 580VNX để giải bài toán trên.
Bài toán xác định nhanh hệ số hàm số bậc 2: Tìm parabol $latex (P):y=a{{x}^{2}}+bx+c$ $latex (a\ne 0)$ biết:
|
Trước hết chúng ta nhắc lại rằng đồ thị của hàm số bậc 2 $latex y=a{{x}^{2}}+bx+c$ $(a\ne 0)$ là một parabol có đỉnh là điểm $latex I\left( -\dfrac{b}{2a};\dfrac{-\Delta }{4a} \right)$ và có trục đối xứng là đường thẳng $latex x=\dfrac{-b}{2a}$.
Lời giải:
a. Ta đã biết nếu đồ thị của $latex (P):y=a{{x}^{2}}+bx+c$ đi qua điểm $latex A({{x}_{A}};{{y}_{A}})$ thì $latex {{y}_{A}}=ax_{A}^{2}+b{{x}_{A}}+c$. Nên từ đó ta có hệ phương trình sau:
$latex \left\{ \begin{align} & -1=a{{.0}^{2}}+b.0+c \\ & -1=a{{.1}^{2}}+b.1+c \\ & 1=a.{{(-1)}^{2}}+b.(-1)+c \\ \end{align} \right.$
$latex \Leftrightarrow \left\{ \begin{align} & c=-1 \\ & a+b+c=-1 \\ & a-b+c=1 \\ \end{align} \right.$
Để giải hệ phương trình 3 ẩn trên máy tính cầm tay CASIO fx 580VNX, ta thực hiện như sau:
Bước 1: Mở chức năng giải hệ phương trình 3 ẩn.
- Cách bấm: w913
- Máy tính hiển thị:
Bước 2: Nhập hệ số của hệ phương trình
- Cách bấm máy tính: 0=0=1=p1=1=1=1=p1=1=p1=1=1=
- Máy tính hiển thị:
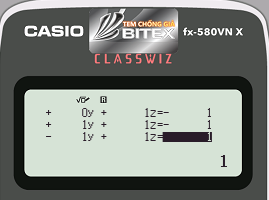
Bước 3: Nhấn phím =
Máy hiển thị nghiệm của hệ là $latex (1;-1;-1)$ nên ta có $latex (P):{{x}^{2}}-x-1$
b. Đồ thị của $latex (P)$ đi qua điểm $latex A(1;2)$, $latex B(2;1)$ và có trục đối xứng là đường thẳng $latex x=1$.
Trục đối xứng của đồ thị hàm số bậc 2 $latex (P)$ là $x=\dfrac{-b}{2a}$. Từ các giả thiết của bài toán ta có hệ phương trình sau:
$latex \left\{ \begin{align} & 2=a{{.1}^{2}}+b.1+c \\ & 1=a{{.2}^{2}}+b.2+c \\ & \frac{-b}{2a}=1 \\ \end{align} \right.$
$latex \Leftrightarrow \left\{ \begin{align} & a+b+c=2 \\ & 4a+2b+c=1 \\ & 2a+b=0 \\ \end{align} \right.$
Thao tác tương tự như ở trên đã trình bày, máy tính cầm tay CASIO fx 580VNX giải ra kết quả:
$\left\{ \begin{align} & a=-1 \\ & b=2 \\ & c=1 \\ \end{align} \right.$
Do đó ta có $latex (P):-{{x}^{2}}+2x+1$
c. Đồ thị của $latex (P)$đi qua $latex D(3,0)$ và có đỉnh $latex I(1;4)$.
Từ các giả thiết của bài toán ta có hệ phương trình sau:
$latex \left\{ \begin{align} & 0=a{{.3}^{2}}+b.3+c \\ & 4=a{{.1}^{2}}+b.1+c \\ & \dfrac{-b}{2a}=1 \\ \end{align} \right.$
$latex \Leftrightarrow \left\{ \begin{align} & 9a+3b+c=0 \\ & a+b+c=4 \\ & 2a+b=0 \\ \end{align} \right.$
Máy tính CASIO fx 580VNX giải hệ trên được kết quả là: $latex a=-1,b=2,c=3$
Vậy $latex (P):-{{x}^{2}}+2x+3$.
Xem thêm sơ lược tính năng nổi trội trên máy tính CASIO fx 580VNX
About Bitex Casio
