BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tóm tắt công thức toạ độ trong mặt phẳng OXY
- 16/08/2022
- 314 lượt xem
⋅ Diện tích tam giác trong mặt phẳng Oxy
$\vec{AB}=(a_{1};a_{2}),\vec{AC}=(b_{1};b_{2})\Rightarrow S_{\Delta ABC}=\frac{1}{2}|a_{1}b_{2}-a_{2}b_{1}|$.
1. Đường thẳng.
a. Các dạng phương trình đường thẳng
− Phương trình tổng quát: $Ax+By+C=0(A^2+B^2>0)$.
(Vec tơ pháp tuyến $\vec{n}=(A;B)$, Vec tơ chỉ phương $\vec{u}=(B;-A)$ hay $\vec{u}=(-B;A)$).
− Phương trình tham số:$\left\{\begin{matrix}.
x=x_{o}+a_{1}t & \\
x=x_{o}+a_{1}t
\end{matrix}\right.$ (t∈R).
(Vec tơ chỉ phương $\vec{n}=(a_{1};a_{2})$ và điểm đi qua $M(x_{0},y_{0})$).
− Phương trình chính tắc: $\frac{x-x_{0}}{a_{1}}=\frac{y-y_{0}}{a_{2}}$.
− Phương trình đoạn chắn: $\frac{x}{a}+\frac{y}{b}=1$.
( đi qua hai điểm A(a;0), B(0;b)).
b. Góc giữa 2 đường thẳng.
− Gọi $\vec{n_{1}}$ và $\vec{n_{2}}$ là hai VTPT của hai đường thẳng $\Delta _{1}$ và $\Delta _{2}$. Khi đó:
$\cos (\Delta _{1},\Delta _{2})=\cos (\vec{n_{1}},\vec{n_{2}})=\frac{|\vec{n_{1}}.\vec{n_{2}}|}{|\vec{n_{1}}|.|\vec{n_{2}}|}=\frac{|a_{1}.a_{2}+b_{1}.b_{2}|}{\sqrt{a_{1}^{2}+a_{1}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}}}$.
c. Khoảng cách từ điểm $M(x_{M};y_{M})$ đến đường thẳng $\Delta:Ax+By+C=0$ là:
$d(M,\Delta)=\frac{|Ax_{M}+By_{M}+C|}{\sqrt{A^2+B^2}}$.
2. Đường tròn.
Các dạng phương trình đường tròn:
− Dạng 1. Phương trình đường tròn (C) có tâm I(a;b) và bán kính R là: $(C):(x-1)^2+(y-b)^2=R^{2}$.
− Dạng 2: Phương trình có dạng: $x^2+y^2-2ax-2by+c=0$ với điều kiện $a^2+b^2-c>0$ là phương trình đường tròn (C) có tâm I(a;b) và bán kính $R=\sqrt{a^2+b^2-c}$.
3. Elip
−Phương trình chính tắc của Elip (E): $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 (a>b)$; $c^2=a^2-b^2$.
−Tiêu điểm:$F_{1}(-c;0),F_{2}(c;0)$.
− Đỉnh trục lớn: $A_{1}(-a;0),A_{2}(a;0)$.
− Đỉnh trục bé: $B_{1}(0;-b),B_{2}(0;b)$.
− Tâm sai: $e=\frac{c}{a}<1$.
− Phương trình đường chuẩn: $x=$±$\frac{a}{e}$.
− Điều kiện tiếp xúc của (E) và $\Delta:Ax+By+C=0$ là: $A^2a^2+B^2b^2=C^2$.
4. Hypebol
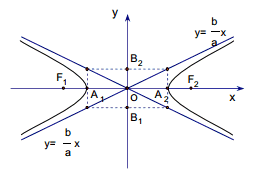
− Phương trình chính tắc (H): $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, $c^2=a^2+b^2$.
− Tiêu điểm $F_{1}(-c;0),F_{2}(c;0)$.
− Đỉnh trên trục thực $A_{1}(-a;0),A_{2}(a;0)$.
− Tâm sai: $e=\frac{c}{a}$.
− Phương trình đường chuẩn: $x=$±$\frac{a}{e}$.
− Điều kiện tiếp xúc của (H) và $\Delta:Ax+By+C=0$ là: $A^2a^2-B^2b^2=C^2$.
5. Parabol.
− Phương trình chính tắc(P): $y^2=2px$.
− Tiêu điểm: $F\left ( \frac{p}{2};0 \right )$.
− Phương trình đường chuẩn: $x=-\frac{p}{2}$.
− Điều kiện tiếp xúc của (P) và $\Delta:Ax+By+C=0$ là: $2AC=B^2p$.
Kết luận: Bài viết giúp bạn thống kê lại những công thức toán lớp 10 chương toạ độ trong mặt phẳng Oxy cần nhớ. Hi vọng bài viết này sẽ như 1 cuốn sổ tay công thức giúp bạn học tốt môn toán lớp 10 hơn.
About Toanbitexdtgd1
