PHƯƠNG TRÌNH ĐƯỜNG TRÒN - PHẦN 1

KIẾN THỨC CHUNG

1. Phương trình đường tròn

Phương trình đường tròn có tâm $I(a;b)$ và bán kính $R$: $\mathbf{(x-a)^2+(y-b)^2=R^2}$

Nhận xét: Phương trình $\mathbf{x^2+y^2+2ax+2by+c=0}$, với $a^2+b^2-c>0$, là phương trình đường tròn tâm $I(-a;-b)$, bán kính $R=\sqrt{a^2+b^2-c}$

2. Phương trình tiếp tuyến của đường tròn

Cho đường tròn $(C)$ có tâm $I$, bán kính $R$ và đường thẳng $\Delta$

$\mathbf{\Delta}$ tiếp xúc với $\mathbf{(C)\iff{}d(I,\Delta)=R}$

 

VẤN ĐỀ 1: Xác định tâm và bán kính của đường tròn

Nếu phương trình đường tròn $(C)$ có dạng: $\mathbf{(x-a)^2+(y-b)^2=R^2}$ thì $(C)$ có tâm $I(a;b)$ và bán kính $R$

Nếu phương trình đường tròn $(C)$ có dạng: $\mathbf{x^2+y^2+2ax+2by+c=0}$ thì biến đổi về dạng $\mathbf{(x-a)^2+(y-b)^2=R^2}$ hoặc tâm $I(-a;-b)$, bán kính $R=\sqrt{a^2+b^2-c}$

Chú ý: Phương trình $\mathbf{x^2+y^2+2ax+2by+c=0}$ là phương trình đường tròn nếu thỏa mãn điều kiện: $a^2+b^2-c>0$

Bài tập 1:

Tìm $m$ để phương trình sau là phương trình đường tròn:

$$x^2+y^2-2(m-3)x+4my-m^2+5m+4=0       (1)$$

Để phương trình $(1)$ là phương trình đường tròn thì

$(m-3)^2+(2m)^2-(-m^2+5m+4)>0$

$\iff{}6m^2-11m+5>0$

$\iff{}\left\{ \begin{array}{l}{x<\dfrac{5}{6}}\\{x>1}\end{array} \right.$

Vậy phương trình $(1)$ là phương trình đường tròn nếu $m$ thỏa $(-\infty;\dfrac{5}{6})\bigcup(1;+\infty)$.

Thao tác thực hiện trên máy tính Casio Fx-580VN X

Chọn chức năng giải bất phương trình: wz21

 

 

VẤN ĐỀ 2: Lập phương trình đường tròn

Để lập phương trình đườn tròn $(C)$ ta thường cần phải xác định tâm $\mathbf{I(a;b)}$ và bán kính $\mathbf{R}$ của $(C)$. Khi đó phương trình đường tròn $(C)$ là:

$$\mathbf{(x-a)^2+(y-b)^2=R^2}$$

 

Dạng 1: $(C)$ có tâm $I$ và đi qua điểm $A$

• Bán kính $R=IA$

Bài tập 1:

Viết phương trình đường tròn có tâm $I$ và đi qua điểm $A$ với: $I(2;4), A(-1;3)$

Bán kính $R=IA=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\sqrt{10}$

Phương trình đường tròn có tâm $I$ và đi qua điểm $A$ là:

$$(x-2)^2+(y-4)^2=10$$

 

Dạng 2: $(C)$ có tâm $I$ và tiếp xúc với đường thẳng $\Delta$

• Bán kính $R=d(I,\Delta)$

Bài tập 2: Viết phương trình đường tròn có tâm $I$ và tiếp xúc với đường thẳng $\Delta$ với: $I(3;4), \Delta:4x-3y+15=0$

Bán kính $R=d(I,\Delta)=\dfrac{|a{x_I}+b{y_I}+c|}{\sqrt{a^2+b^2}}=3$

Phương trình đường tròn có tâm $I$ và tiếp xúc với đường thẳng $\Delta$ là:

$$(x-3)^2+(y-4)^2=9$$

 

Dạng 3: $(C)$ có đường kính $AB$

• Tâm $I$ là trung điểm của $AB$
• Bán kính $R=\dfrac{AB}{2}$

Bài tập 3: Viết phương trình đường tròn có đường kính $AB$ với $A(-2;3), B(6;5)$

Tâm $I=(\dfrac{{x_A}+{x_B}}{2};\dfrac{{y_A}+{y_B}}{2})=(2;4)$

Bán kính $R=\dfrac{AB}{2}=\dfrac{\sqrt{({x_B}-{x_A})^2+({y_B}-{y_A})^2}}{2}=\sqrt{17}$

Phương trình đường tròn có đường kính $AB$

$$(x-2)^2+(y-4)^2=17$$

 

Dạng 4: $(C)$ đi qua hai điểm $A, B$ và có tâm $I$ nằm trên đường thẳng $\Delta$

• Viết phương trình đường trung trực $d$ của đoạn $AB$
• Xác định tâm $I$ là giao điểm của $d$ và $\Delta$
• Bán kính $R=IA$

Bài tập 4: Viết phương trình đường tròn đi qua hai điểm $A, B$ và có tâm $I$ nằm trên đường thẳng $\Delta$ với $A(2;3), B(-1;1), \Delta{x-3y-11=0}$

Gọi $M$ là trung điểm của đoạn $AB$. Tọa độ điểm $M$ là $(\dfrac{{x_A}+{x_B}}{2};\dfrac{{y_A}+{y_B}}{2})=(\dfrac{1}{2};2)$

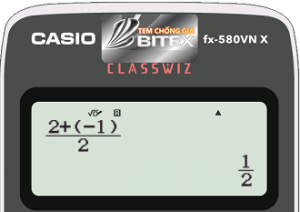
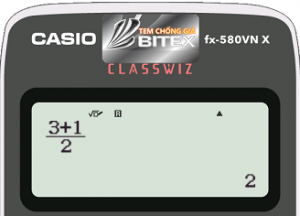
Vector pháp tuyến của đường thẳng $d$ là $\overrightarrow{\rm AB}=({x_B}-{x_A};{y_B}-{y_A})=(-3;-2)$

Phương trình đường trung trực $d$ của đoạn $AB$ đi qua điểm $M$ là:

$(d): -3(x-\dfrac{1}{2})-2(y-2)=0$

$\iff{}(d): 6x+4y-11=0$

Tâm $I$ là giao điểm của $d$ và $\Delta$: $\left\{ \begin{array}{l}{6x+4y=11\\x-3y=11}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{{x=\dfrac{7}{2}}\\{y=-\dfrac{5}{2}}}\end{array}\right.$

Bán kính $R=IA=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\dfrac{\sqrt{130}}{2}$

Phương trình đường tròn đi qua hai điểm $A, B$ và có tâm $I$ nằm trên đường thẳng $\Delta$ là:

$$(x-\dfrac{7}{2})^2+(y+\dfrac{5}{2})^2=\dfrac{65}{2}$$

 

Dạng 5: $(C)$ đi qua hai điểm $A, B$ và tiếp xúc với đường thẳng $\Delta$

• Viết phương trình đường trung trực $d$ của đoạn $AB$
• Tâm $I$ của $(C)$ thoả mãn: $\left\{ \begin{array}{l}{{I\in{d}}\\{d(I,\Delta)=IA}}\end{array}\right.$
• Bán kính $R=IA$

Bài tập 5: Viết phương trình đường tròn đi qua hai điểm $A, B$ và tiếp xúc với đường thẳng $\Delta$ với:  $A(1;2), B(3;4), \Delta{3x+y-3}$

Gọi $M$ là trung điểm của đoạn $AB$. Tọa độ điểm $M$ là $(\dfrac{{x_A}+{x_B}}{2};\dfrac{{y_A}+{y_B}}{2})=(2;3)$

Vector pháp tuyến của đường thẳng $d$ là $\overrightarrow{\rm AB}=({x_B}-{x_A};{y_B}-{y_A})=(2;2)$

Phương trình đường trung trực $d$ của đoạn $AB$ đi qua điểm $M$ là:

$(d): 2(x-2)+2(y-3)=0$

$\iff{}(d): x+y-5=0$

Tâm $I$ của $(C)$ thoả mãn:

$\left\{ \begin{array}{l}{{I\in{d}}\\{d(I,\Delta)=IA}}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{{x_I}+{y_I}=5}\\{\dfrac{|a{x_I}+b{y_I}+c|}{\sqrt{a^2+b^2}}}={\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{{x_I}+{y_I}=5}\\{\dfrac{|3{x_I}+{y_I}-3|}{\sqrt{10}}}={\sqrt{({1}-{x_I})^2+({2}-{y_I})^2}}\end{array}\right.$

$\iff{}\left[ \begin{array}{l}{x=4}\\{x=\dfrac{3}{2}}\end{array}\right.$

Ta có $2$ tọa độ $I$ thỏa yêu cầu bài toán với: $I(4;1)$ và $I(\dfrac{3}{2};\dfrac{7}{2})$

Bán kính khi $I(4;1)$ $R=IA=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\sqrt{10}$

Bán kính khi $I(\dfrac{3}{2};\dfrac{7}{2})$ $R=IA=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\dfrac{\sqrt{10}}{2}$

Phương trình đường tròn đi qua hai điểm $A, B$ và tiếp xúc với đường thẳng $\Delta$ có tâm $I(4;1)$ và bán kính $R=\sqrt{10}$ là:

$$(x-4)^2+(y-1)^2=10$$

Phương trình đường tròn đi qua hai điểm $A, B$ và tiếp xúc với đường thẳng $\Delta$ có tâm $I(\dfrac{3}{2};\dfrac{7}{2})$ và bán kính $R=\dfrac{\sqrt{10}}{2}$ là:

$$(x-\dfrac{3}{2})^2+(y-\dfrac{7}{2})^2=\dfrac{5}{2}$$

 

Dạng 6: $(C)$ đi qua điểm $A$ và tiếp xúc với đường thẳng $\Delta$ tại điểm $B$

• Viết phương trình đường trung trực $d$ của đoạn $AB$
• Viết phương trình đường thẳng $\Delta’$ đi qua $B$ và vuông góc với $\Delta$
• Xác định tâm $I$ là giao điểm của $d$ và $\Delta’$
• Bán kính $R=IA$

Bài tập 6: Viết phương trình đường tròn đi qua điểm $A$ và tiếp xúc với đường thẳng $\Delta$ tại điểm $B$, với $A(-2;6), \Delta{3x-4y-15=0}, B(1;-3)$

Gọi $M$ là trung điểm của đoạn $AB$. Tọa độ điểm $M$ là $(\dfrac{{x_A}+{x_B}}{2};\dfrac{{y_A}+{y_B}}{2}=(-\dfrac{1}{2};\dfrac{3}{2})$

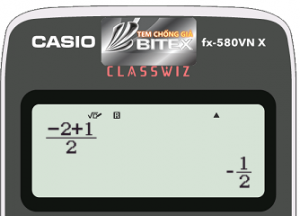
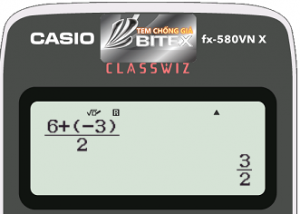
Vector pháp tuyến của đường thẳng $d$ là $\overrightarrow{\rm AB}=({x_B}-{x_A};{y_B}-{y_A})=(3;-9)$

Phương trình đường trung trực $d$ của đoạn $AB$ đi qua điểm $M$ là:

$(d): 3(x+\dfrac{1}{2})-9(y-\dfrac{3}{2})=0$

$\iff{}(d): x-3y+5=0$

Phương trình đường thẳng $\Delta’$ đi qua $B$ và vuông góc với $\Delta$ là:

$(\Delta’): 3(x-1)-4(y+3)=0$

$\iff{}(\Delta’): 3x-4y-15=0$

Tâm $I$ là giao điểm của $d$ và $\Delta’$

$\left\{ \begin{array}{l}{x-3y=-5\\3x-4y=15}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{x=13\\y=6}\end{array}\right.$

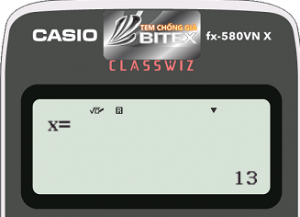
Bán kính $R=IA=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=15$

Phương trình đường tròn đi qua điểm $A$ và tiếp xúc với đường thẳng $\Delta$ tại điểm $B$, với $A(-2;6), \Delta{3x-4y-15=0}, B(1;-3)$ là:

$$(x-13)^2+(y-6)^2=225$$

 

Dạng 7: $(C)$ đi qua điểm $A$ và tiếp xúc với hai đường thẳng ${\Delta_1}$ và ${\Delta_2}$

• Tâm $I$ của $(C)$ thỏa mãn: $\left\{ \begin{array}{l}{d(I,{\Delta_1})=d(I,{\Delta_2})   (1)}\\{d(I,{\Delta_1})=IA   (2)}\end{array}\right.$
• Bán kính $R=IA$

Chú ý: – Muốn bỏ dấu giá trị tuyệt đối trong $(1)$, ta xét dấu miền mặt phẳng định bởi ${\Delta_1}$ và ${\Delta_2}$ hay xét dấu khoảng cách đại số từ $A$ đến ${\Delta_1}$ và ${\Delta_2}$

– Nếu ${\Delta_1}//{\Delta_2}$, ta tính $R=\dfrac{1}{2}d({\Delta_1},{\Delta_2})$, và $(2)$ được thay thế bởi $IA=R$

Bài tập 7: Viết phương trình đường tròn đi qua điểm $A$ và tiếp xúc với hai đường thẳng ${\Delta_1}$ và ${\Delta_2}$ với $A(2;3), {\Delta_1}:{3x-4y+1=0}, {\Delta_2}:{4x+3y-7=0}$

Tâm $I$ thỏa mãn:

$\left\{ \begin{array}{l}{d(I,{\Delta_1})=d(I,{\Delta_2})   (1)}\\{d(I,{\Delta_1})=IA   (2)}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{\dfrac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}}={\dfrac{|{a_2}{x_I}+{b_2}{y_I}+{c_2}|}{\sqrt{{a_2}^2+{b_2}^2}}}\\{\dfrac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}}={\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{x+7y-8=0}\\{4x^2+11y^2+26x+22y-24xy-64=0}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{x=8-7y}\\{375y^2-800y+400=0}\end{array}\right.$

Với tâm $I(-\dfrac{4}{3};\dfrac{4}{3})$ thì $R=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\dfrac{{5}{\sqrt{5}}}{3}$

Phương trình đường tròn đi qua điểm $A$ và tiếp xúc với hai đường thẳng ${\Delta_1}$ và ${\Delta_2}$ với $A(2;3), {\Delta_1}:{3x-4y+1=0}, {\Delta_2}:{4x+3y-7=0}$ là:

$$(x+\dfrac{4}{3})^2+(y-\dfrac{4}{3})^2=\dfrac{125}{9}$$

Với tâm $I(\dfrac{12}{5};\dfrac{4}{5})$ thì $R=\sqrt{({x_A}-{x_I})^2+({y_A}-{y_I})^2}=\sqrt{5}$

Phương trình đường tròn đi qua điểm $A$ và tiếp xúc với hai đường thẳng ${\Delta_1}$ và ${\Delta_2}$ với $A(2;3), {\Delta_1}:{3x-4y+1=0}, {\Delta_2}:{4x+3y-7=0}$ là:

$$(x-\dfrac{12}{5})^2+(y-\dfrac{4}{5})^2=5$$

 

Dạng 8: $(C)$ tiếp xúc với hai đường thẳng ${\Delta_1},{\Delta_2}$ và có tâm nằm trên đường thẳng $d$

• Tâm $I$ của $(C)$ thỏa mãn: $\left\{ \begin{array}{l}{d(I,{\Delta_1})=d(I,{\Delta_2})}\\{I\in{d}}\end{array}\right.$
• Bán kính $R=d(I,{\Delta_1})$

Bài tập 8: Viết phương trình đường tròn tiếp xúc với hai đường thẳng ${\Delta_1},{\Delta_2}$ và có tâm nằm trên đường thẳng $d$ với: ${\Delta_1}:{3x+2y+3=0}, {\Delta_2}:{2x-3y+15=0}, d: x-y=0$

Tâm $I$ thỏa mãn:

$\left\{ \begin{array}{l}{d(I,{\Delta_1})=d(I,{\Delta_2})}\\{I\in{d}}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{\dfrac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}}={\dfrac{|{a_2}{x_I}+{b_2}{y_I}+{c_2}|}{\sqrt{{a_2}^2+{b_2}^2}}}\\{I\in{d}}\end{array}\right.$

$\iff{}\left[ \begin{array}{l}{\left\{ \begin{array}{l}{x+5y-12=0}\\{x-y=0}\end{array}\right.}\\{\left\{ \begin{array}{l}{5x-y+18=0}\\{x-y=0}\end{array}\right.}\end{array}\right.$

$\iff{}\left[ \begin{array}{l}{x=y=2}\\{x=y=-\dfrac{9}{2}}\end{array}\right.$

Bán kính khi $I(2;2) R=d(I,{\Delta_1})=\dfrac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}=\sqrt{13}$

Bán kính khi $I(-\dfrac{9}{2};-\dfrac{9}{2}) R=d(I,{\Delta_1})=\dfrac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}=\dfrac{{3}\sqrt{13}}{2}$

Phương trình đường tròn tiếp xúc với hai đường thẳng ${\Delta_1},{\Delta_2}$ và có tâm nằm trên đường thẳng $d$ với: ${\Delta_1}:{3x+2y+3=0}, {\Delta_2}:{2x-3y+15=0}, d: x-y=0$ có tâm $I(2;2)$ và bán kính $R=\sqrt{13}$ là:

$$(x-2)^2+(y-2)^2=13$$

Phương trình đường tròn tiếp xúc với hai đường thẳng ${\Delta_1},{\Delta_2}$ và có tâm nằm trên đường thẳng $d$ với: ${\Delta_1}:{3x+2y+3=0}, {\Delta_2}:{2x-3y+15=0}, d: x-y=0$ có tâm $I(-\dfrac{9}{2};-\dfrac{9}{2})$ và bán kính $R=\dfrac{{3}\sqrt{13}}{2}$ là:

$$(x+\dfrac{9}{2})^2+(y+\dfrac{9}{2})^2=\dfrac{117}{4}$$

 

Dạng 9: $(C)$ đi qua ba điểm không thẳng hàng $A, B,C$ (đường tròn ngoại tiếp tam giác)

Cách 1:

• Phương trình của $(C)$ có dạng: $x^2+y^2+2ax+2by+c=0$   $(*)$
• Lần lượt thay tọa độ của $A, B, C$ vào $(*)$ ta được hệ phương trình
• Giải hệ phương trình này ta tìm được $a, b, c$ $\rightarrow$ phương trình của $(C)$

Cách 2:

• Tâm $I$ của $(C)$ thỏa mãn:  $\left\{ \begin{array}{l}{IA=IB\\IA=IC}\end{array}\right.$
• Bán kính $R=IA=IB=IC$

Bài tập 9: Viết phương trình đường tròn ngoại tiếp tam giác $ABC$ với: $A(2;0), B(0;-3), C(5;-3)$

Phương trình đường tròn có dạng: $x^2+y^2+2ax+2by+c=0$   $(*)$

Thay tọa của $A, B, C$ vào $(*)$ ta được hệ phương trình:

$\left\{ \begin{array}{l}{4+4a+c=0}\\{9-6b+c=0}\\{34+10a-6b+c=0}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{4+4a+c=0}\\{9-6b+c=0}\\{34+10a-6b+c=0}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{a=-\dfrac{5}{2}\\b=\dfrac{5}{2}\\c=6}\end{array}\right.$

Phương trình đường tròn ngoại tiếp tam giác $ABC$ với: $A(2;0), B(0;-3), C(5;-3)$ là:

$$x^2+y^2-5x+5y+c=0$$

 

Dạng 10: $(C)$ nội tiếp tam giác $ABC$

• Viết phương trình của hai đường phân giác trong của hai góc trong tam giác
• Xác định tâm $I$ là giao điểm của hai đường phân giác trên
• Bán kính $R=d(I,AB)$

Bài tập 10: Viết phương trình đường tròn nội tiếp tam giác $ABC$ với $AB:2x-3y+21=0, BC: 3x-2y-6=0, CA: 2x+3y+9=0$

Phương trình của hai đường phân giác trong của hai góc trong tam giác là:

$\dfrac{{a_2}x+{b_2}y+{c_2}}{\sqrt{{a_2}^2+{b_2}^2}}=\pm\dfrac{{a_3}x+{b_3}y+{c_3}}{\sqrt{{a_3}^2+{b_3}^2}}$

$\iff{}\left[ \begin{array}{l}{3x-2y-6=2x+3y+9}\\{3x-2y-6=-(2x+3y+9)}\end{array}\right.$

$\iff{}\left[ \begin{array}{l}{x-5y-15=0}\\{5x+y+3=0}\end{array}\right.$

Tâm $I$ là giao điểm của hai đường phân giác:

$\left\{ \begin{array}{l}{x-5y-15=0}\\{5x+y+3=0}\end{array}\right.$

$\iff{}\left\{ \begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$

Bán kính $R=d(I,AB)=\frac{|{a_1}{x_I}+{b_1}{y_I}+{c_1}|}{\sqrt{{a_1}^2+{b_1}^2}}=\dfrac{30}{\sqrt{13}}$

Phương trình đường tròn nội tiếp tam giác $ABC$ với $AB:2x-3y+21=0, BC: 3x-2y-6=0, CA: 2x+3y+9=0$ là:

$$x^2+(y+3)^2=\dfrac{900}{13}$$

About Toanbitexdtgd1

Bài viết liên quan

ĐỀ THI THAM KHẢO VÀ CHÍNH THỨC THPT QUỐC GIA 5 NĂM GẦN ĐÂY (NĂM 2019 – 2023)

4 tuần Trước

BỘ ĐỀ THI HKII LỚP 10

19/03/2024

Giải 5 câu trắc nghiệm Đ/S lớp 11 của SGD Hà Nội – 2

18/03/2024

Giải 5 câu trắc nghiệm Đ/S lớp 11 của SGD Hà Nội – 5

18/03/2024

Giải 5 câu trắc nghiệm Đ/S lớp 11 của SGD Hà Nội – 3

18/03/2024

Giải 5 câu trắc nghiệm Đ/S lớp 11 của SGD Hà Nội – 1

18/03/2024